CHAPITRE 5 :LES ATTRACTEURS ETRANGES
FICHIER MAPLE CORRESPONDANT : ATTRACTEURS.MWS
A ] Définition
Une fois n'est pas coutume, nous allons donner d'emblée une définition de ce qu'on appelle un attracteur étrange. Comme d'habitude, cette définition n'est pas encore définitivement "homologuée" dans le milieu scientifique. Elle sera donnée pour un attracteur étrange dans l'espace. Pour un système dynamique dans le plan, il suffit de remplacer boule par disque, et pour un système dynamique ne dépendant que d'une coordonnée, par intervalle.
Un sous-ensemble borné  de l'espace est un attracteur étrange et chaotique pour une transformation
de l'espace est un attracteur étrange et chaotique pour une transformation  de l'espace s'il existe un voisinage
de l'espace s'il existe un voisinage  de
de  (c'est à dire que pour tout point de
(c'est à dire que pour tout point de  il existe une boule contenant ce point et contenue dans
il existe une boule contenant ce point et contenue dans  ) vérifiant les propriétés suivantes :
) vérifiant les propriétés suivantes :
1) Attraction :  est une zone de capture, ce qui signifie que toute orbite par
est une zone de capture, ce qui signifie que toute orbite par  dont le point initial est dans
dont le point initial est dans  , est entièrement contenue dans
, est entièrement contenue dans  . De plus, toute orbite de ce type devient et reste aussi proche de
. De plus, toute orbite de ce type devient et reste aussi proche de  que l'on veut.
que l'on veut.
2) Sensibilité : les orbites dont le point initial est dans  sont extrêmement sensibles aux conditions initiales, au sens où cela a été défini dans le chapitre 2 ; ceci traduit un comportement chaotique.
sont extrêmement sensibles aux conditions initiales, au sens où cela a été défini dans le chapitre 2 ; ceci traduit un comportement chaotique.
3) Fractal :  est un objet fractal, ce qui justifie l'adjectif étrange.
est un objet fractal, ce qui justifie l'adjectif étrange.
4) Mélange : pour tout point de  , il existe des orbites démarrées dans
, il existe des orbites démarrées dans  , et qui passent aussi près que l'on veut de ce point.
, et qui passent aussi près que l'on veut de ce point.
Cette définition s'applique à un certain nombre d'objets déjà rencontrés :
- L'attracteur de l'itérateur quadratique au point de Feigenbaum (voir chapitre 4) est un fractal linéaire de type ensemble de Cantor, vérifiant les propriétés ci-dessus en prenant par exemple  . (attention, les attracteurs pour les autres valeurs de
. (attention, les attracteurs pour les autres valeurs de  sont soit périodiques, donc ne vérifient pas la propriété 2), soit égaux à une réunion d'intervalles, et donc ne vérifient pas 3))
sont soit périodiques, donc ne vérifient pas la propriété 2), soit égaux à une réunion d'intervalles, et donc ne vérifient pas 3))
- Le tamis de Sierpinski est un fractal plan dont tout ce qu'on en a vu tend à prouver que c'est un attracteur étrange pour l'IFS correspondant. En particulier, la notion de mélange a été utilisée pour reconstruire rapidement une image de l'attracteur, grâce à l'ergodicité des orbites. Pour  , on peut proposer le triangle initial.
, on peut proposer le triangle initial.
Il en est de même pour les autres attracteurs d'IFS étudiés dans le chapitre 3, bien que dans les autres cas, l'exhibition d'une zone de capture soit moins évidente.
Dans la suite de ce chapitre, nous allons montrer quelques attracteurs étranges classiques.
B ] L'attracteur de Hénon
C'est un exemple d'attracteur étrange dans le plan, qui aurait pu trouver sa place parmi les attracteurs étudiés dans le chapitre 3. Sa particularité provient de ce que l'IFS qui lui correspond ne comporte qu'une seule transformation, ce qui permet de le considérer comme l'attracteur d'un système dynamique dans le plan (au lieu de l'espace métrique des compacts du plan). D'autre part, l'ergodicité des orbites fait qu'une procédure analogue à la procédure IFS_ergodique permet, sans utiliser de probabilités, d'obtenir facilement une construction graphique de l'attracteur.
Il s'agit bien entendu de la procédure hénon. Cette procédure permet de construire en fait une famille d'attracteurs dépendant de deux paramètres. Les paramètres proposés à l'origine par Hénon sont  .
.
Un excellent exercice serait de retrouver cet attracteur par l'IFS à une seule transformation initiée à un triangle, comme dans le chapitre 3.
Essayons de voir pourquoi l'attracteur de Hénon pour  satisfait aux propriétés définitoires d'un attracteur étrange :
satisfait aux propriétés définitoires d'un attracteur étrange :
1) Un bon mélange
C'est la propriété qui apparaît le plus clairement, puisque c'est l'ergodicité elle-même des orbites qui permet de construire une vue de l'attracteur. Si le point initial est modifié, l'orbite change aussi, mais l'aspect général de l'orbite - c'est à dire l'attracteur - reste inchangé.
2) Une zone de capture
On constate déjà sur le graphique hénon(0,0,pas,1.4,.3) que le point initial  est en dehors de l'attracteur. Son orbite approxime néanmoins l'attracteur : on peut donc le considérer comme un point d'une zone de capture éventuelle. Et en effet, Hénon a proposé comme zone de capture
est en dehors de l'attracteur. Son orbite approxime néanmoins l'attracteur : on peut donc le considérer comme un point d'une zone de capture éventuelle. Et en effet, Hénon a proposé comme zone de capture  un quadrilatère que l'on peut visualiser grâce à la commande display qui suit. L'attracteur a été réesquissé pour montrer son inclusion dans cette zone. On constate alors que des points très proches de l'attracteur sont exclus de ce quadrilatère. En prenant le point (1.292;0), on s'aperçoit en effet que son orbite s'éloigne indéfiniment. Avec hénon(1.292,0,20,1.4,.3), on obtient des coordonnées trop grandes en valeur absolue lors des calculs, et un message d'erreur s'affiche.
un quadrilatère que l'on peut visualiser grâce à la commande display qui suit. L'attracteur a été réesquissé pour montrer son inclusion dans cette zone. On constate alors que des points très proches de l'attracteur sont exclus de ce quadrilatère. En prenant le point (1.292;0), on s'aperçoit en effet que son orbite s'éloigne indéfiniment. Avec hénon(1.292,0,20,1.4,.3), on obtient des coordonnées trop grandes en valeur absolue lors des calculs, et un message d'erreur s'affiche.
Ce phénomène permet d'introduire une notion intéressante : celle de bassin d'attraction d'un attracteur. Il s'agit de l'ensemble des points initiaux dont l'orbite finit par entrer dans une zone de capture. On peut remarquer que le bassin d'attraction est indépendant de la zone de capture choisie, puisqu'une fois dans une telle zone, l'orbite se rapproche indéfiniment de l'attracteur. Les bassins d'attraction sont souvent imprévisibles. La procédure bassin_hénon permet de tester l'appartenance d'un point au bassin d'attraction de l'attracteur de Hénon. Ce test n'est théoriquement pas infaillible, puisqu'il ne porte que sur l'appartenance d'un itéré de rang fini à la zone de capture. Mais en pratique, si l'orbite ne converge pas vers l'attracteur, elle diverge très rapidement, et MAPLE sort un message d'impuissance dans le calcul. On pourra tester l'appartenance des points proposés au bassin d'attraction de l'attracteur de Hénon, et constater en observant sa section par la droite  qu'il n'a pas une forme évidente a priori.
qu'il n'a pas une forme évidente a priori.
3) Une structure fractale
La transformation de Hénon  a pour jacobien en
a pour jacobien en  le déterminant
le déterminant  . Il en résulte que si
. Il en résulte que si  , on peut considérer que chaque application à un sous-ensemble du plan de la transformation de Hénon réduit son aire du facteur
, on peut considérer que chaque application à un sous-ensemble du plan de la transformation de Hénon réduit son aire du facteur  . Dans le cas
. Dans le cas  , et sachant que l'on peut aussi considérer l'attracteur de Hénon comme l'attracteur d'un IFS, on en déduit que si l'on part initialement d'une forme géométrique quelconque, par exemple un triangle, l'attracteur aura à la limite une aire nulle.
, et sachant que l'on peut aussi considérer l'attracteur de Hénon comme l'attracteur d'un IFS, on en déduit que si l'on part initialement d'une forme géométrique quelconque, par exemple un triangle, l'attracteur aura à la limite une aire nulle.
L'attracteur de Hénon est donc d'aire nulle. Pour visualiser sa structure fractale, nous allons en zoomer une partie en modifiant la procédure hénon de manière à travailler dans des intervalles d'abscisses et d'ordonnées plus petits. C'est la procédure zoom_hénon, dans laquelle on prend l'origine comme point initial, et où on s'impose de construire 200 points. Les deux zooms successifs proposés montrent clairement que ce qui apparaît à l'il comme une ligne est en fait composé de lignes plus petites, qui a leur tour sont composées de lignes encore plus petites, et ainsi de suite...
Ceci est un effet d'auto-similitude statistique. En fait, une section de l'attracteur de Hénon donne un ensemble de type ensemble de Cantor. L'attracteur de Hénon ressemble à un ensemble de Cantor de lignes. C'est donc bien un fractal, et sa dimension de recouvrement a d'ailleurs été estimée à environ .
.
4) La sensibilité
Pour la tester, il faudrait prendre deux points initiaux arbitrairement proches dans le bassin d'attraction, et comparer leurs orbites. Mais, même en prenant deux couleurs différentes, on ne verrait que deux attracteurs de Hénon quasiment superposés, ce qui pourrait même laisser à penser qu'en fait les orbites restent liées !
Une meilleure façon de faire est de construire l'ensemble des points  , où
, où  est la suite des abscisses des itérés par la transformation de Hénon d'un certain point, tandis que
est la suite des abscisses des itérés par la transformation de Hénon d'un certain point, tandis que  est la suite des abscisses des itérés d'un autre point, pris très proche du premier (on pourrait naturellement faire la même chose sur les ordonnées).
est la suite des abscisses des itérés d'un autre point, pris très proche du premier (on pourrait naturellement faire la même chose sur les ordonnées).
Si l'on obtenait une répartition particulière de ces points, par exemple une courbe, on pourrait conclure à une corrélation entre les orbites. Par contre, si les points obtenus se répartissent un peu partout dans le carré des possibilités (n'oublions pas que l'attracteur de Hénon étant borné, le domaine des abscisses l'est aussi. D'autre part, il apparaît sur le graphique hénon(0,0,pas,1.4,.3) que ce domaine est dense dans un intervalle ( )).
)).
Le tracé correspondant est obtenu par la procédure sensibilité_hénon(point1,point2,n), et montre à l'évidence une indépendance complète des orbites, au moins après quelques itérations. Les régions plus denses correspondent bien évidemment aux endroits plus "étroits" de l'attracteur de Hénon, autour de  .
.
Maintenant que nous sommes convaincus que pour les paramètres  , on obtient un attracteur étrange, regardons ce qui se passe pour d'autres valeurs des paramètres : si l'on essaie les choix hénon(0,0,1000,0.3,0.3), hénon(0,0,1000,0.3,0.4), hénon(0,0,1000,1,.3), on s'aperçoit qu'il existe toujours un attracteur, mais qu'il n'a plus rien d'étrange, puisqu'il s'agit d'un ensemble fini formé de un, deux, ou quatre points respectivement !
, on obtient un attracteur étrange, regardons ce qui se passe pour d'autres valeurs des paramètres : si l'on essaie les choix hénon(0,0,1000,0.3,0.3), hénon(0,0,1000,0.3,0.4), hénon(0,0,1000,1,.3), on s'aperçoit qu'il existe toujours un attracteur, mais qu'il n'a plus rien d'étrange, puisqu'il s'agit d'un ensemble fini formé de un, deux, ou quatre points respectivement !
On retrouve donc des cycles attractifs, comme pour l'itérateur quadratique, à la différence que maintenant ces cycles sont formés de points, au lieu d'être formés de nombres.
Pour essayer d'y voir plus clair, on va fixer  , et on va faire varier
, et on va faire varier  pour obtenir un diagramme de Feigenbaum. Pour pouvoir facilement le comparer avec celui de l'itérateur quadratique, on va étudier une seule variable, à savoir l'abscisse des points de l'orbite. On aurait tout aussi bien pu étudier l'ordonnée, voire la distance à l'origine, cela aurait donné un résultat analogue.
pour obtenir un diagramme de Feigenbaum. Pour pouvoir facilement le comparer avec celui de l'itérateur quadratique, on va étudier une seule variable, à savoir l'abscisse des points de l'orbite. On aurait tout aussi bien pu étudier l'ordonnée, voire la distance à l'origine, cela aurait donné un résultat analogue.
L'appel de procédure itérateur_hénon(0,1.42,pas), analogue à feigenbaum, permet de visualiser les attracteurs des transformations de Hénon lorsque  varie. Et le diagramme obtenu ressemble comme un frère au diagramme obtenu avec feigenbaum ! On retrouve la même entrée vers le chaos par doublement de la longueur des cycles périodiques, les mêmes fenêtres périodiques après le point correspondant au point de Feigenbaum. Et on ne s'étonnera pas d'apprendre que le rapport des écarts consécutifs entre deux bifurcations consécutives dans le diagramme obtenu converge vers la constante universelle de Feigenbaum...
varie. Et le diagramme obtenu ressemble comme un frère au diagramme obtenu avec feigenbaum ! On retrouve la même entrée vers le chaos par doublement de la longueur des cycles périodiques, les mêmes fenêtres périodiques après le point correspondant au point de Feigenbaum. Et on ne s'étonnera pas d'apprendre que le rapport des écarts consécutifs entre deux bifurcations consécutives dans le diagramme obtenu converge vers la constante universelle de Feigenbaum...
Il y a cependant une nouveauté : aux alentours de  , il semble y avoir coexistence de plusieurs attracteurs différents. C'est pour permettre de voir cela que la procédure est si complexe : il y a essai de vingt points initiaux différents pour chaque paramètre, par balayage sur l'ordonnée autour de
, il semble y avoir coexistence de plusieurs attracteurs différents. C'est pour permettre de voir cela que la procédure est si complexe : il y a essai de vingt points initiaux différents pour chaque paramètre, par balayage sur l'ordonnée autour de  ; s'il y a dépassement dans les calculs, cela signifie que le point n'est dans aucun bassin d'attraction. Sinon, on ajoute son orbite à l'ensemble des points à dessiner. Ceci est nécessaire dans la mesure où on ignore comment est situé le bassin d'attraction de chaque attracteur. Pour limiter le cardinal de l'ensemble des points à tracer, on travaille modulo
; s'il y a dépassement dans les calculs, cela signifie que le point n'est dans aucun bassin d'attraction. Sinon, on ajoute son orbite à l'ensemble des points à dessiner. Ceci est nécessaire dans la mesure où on ignore comment est situé le bassin d'attraction de chaque attracteur. Pour limiter le cardinal de l'ensemble des points à tracer, on travaille modulo  .
.
Mais revenons à la coexistence de plusieurs attracteurs. A priori, il pourrait s'agir d'un seul attracteur, le diagramme obtenu manquant de précision suffisant pour s'en assurer.
Mais la construction simultanée, à l'aide de display(hénon1(...),hénon2(...)), permet de bien voir que les orbites de deux points distincts fournissent deux attracteurs distincts.
C ] Les systèmes dynamiques continus
Jusqu'à présent, nous avons exclusivement étudié des systèmes dynamiques discrets, c'est à dire définis par une application  d'un sous-ensemble
d'un sous-ensemble  d'un espace métrique dans lui-même, et la "formule"
d'un espace métrique dans lui-même, et la "formule"  .
.
Dans un premier temps, supposons que  soit une fonction de
soit une fonction de  . En modifiant quelque peu les notations, on a donc
. En modifiant quelque peu les notations, on a donc  , dont la première égalité peut s'écrire
, dont la première égalité peut s'écrire  . Dans ce processus dynamique, on passe d'un itéré au suivant en incrémentant
. Dans ce processus dynamique, on passe d'un itéré au suivant en incrémentant  de 1 à chaque fois. Imaginons maintenant qu'on l'incrémente d'une fraction seulement de 1, soit
de 1 à chaque fois. Imaginons maintenant qu'on l'incrémente d'une fraction seulement de 1, soit  . On obtient
. On obtient  . Lorsque
. Lorsque  , tout élève de terminale dit que
, tout élève de terminale dit que  . Cette audacieuse manoeuvre doit sa réussite au fait que l'on considère dorénavant
. Cette audacieuse manoeuvre doit sa réussite au fait que l'on considère dorénavant  comme une fonction d'une variable
comme une fonction d'une variable 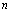 , et que l'on étudie précisément cette fonction en un point qui s'appelle aussi
, et que l'on étudie précisément cette fonction en un point qui s'appelle aussi 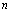 ! Le rapport
! Le rapport  ne dépendait que du point
ne dépendait que du point 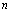 , alors que
, alors que  , lui, dépend du point
, lui, dépend du point  et de la fonction
et de la fonction 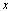 . On est donc amené à écrire
. On est donc amené à écrire  , ou encore, en posant
, ou encore, en posant  :
:  .
.
En récupérant la condition initiale, on parvient à ce qu'on appelle une équation différentielle :  .
.
On dit qu'une telle équation détermine un système dynamique continu.
Le passage du système discret au système continu, tel qu'il a été décrit ci-dessus, représente assez fidèlement l'évolution des mathématiques qui a amené à la notion d'équation différentielle. En effet, dans la pratique, l'étude d'un système dynamique (le mouvement d'un astre, par exemple) se fait par une collection d'observations discrètes régulièrement espacées dans le temps. Ce système dynamique est donc naturellement perçu comme un système discret, même lorsqu'on sait qu'il subit une évolution continue. La méthode ci-dessus consiste donc à imaginer ce qui se passerait à la limite si on faisait des observations consécutives de plus en plus rapprochées.
Cette méthode a d'ailleurs aussi donné naissance au calcul intégral, l'intégrale étant considérée comme la limite d'une somme d'éléments dont la taille tend vers zéro et le nombre vers l'infini.
Le développement de l'analyse différentielle a dès lors permis d'immenses progrès dans la compréhension de systèmes continus que, jusqu'alors, on ne pouvait appréhender que de manière discrète : grosso modo, une orbite composée d'un nombre dénombrable de points est remplacée par une courbe continue.
Réciproquement, les systèmes discrets permettent un calcul approché effectif des solutions de presque tous les systèmes continus, ceux dont on ne sait pas trouver une solution explicite de l'équation différentielle. C'est notamment le cas de toutes les méthodes de constructions de solutions de telles équations par des ordinateurs : les célèbres méthodes d'Euler et de Runge-Kutta ne sont que des discrétisations de systèmes dynamiques continus.
Naturellement, l'exemple simple développé ci-dessus possède de nombreuses généralisations.
Par exemple, si le système discret est de la forme  , alors le système continu correspondant sera de la forme
, alors le système continu correspondant sera de la forme  , ce qui est la forme habituelle d'une équation différentielle ordinaire du premier ordre.
, ce qui est la forme habituelle d'une équation différentielle ordinaire du premier ordre.
De même, si on a un système vectoriel discret,  , on obtient un système d'équations différentielles
, on obtient un système d'équations différentielles  , et ainsi de suite...
, et ainsi de suite...
Attention pourtant : tout système discret ne peut pas être transformé de façon satisfaisante en un système continu (alors que l'inverse est vrai). Intuitivement, il faut que sa dynamique sous-jacente soit continue (dépendant par exemple continûment du temps). Un phénomène purement discret peut avoir une interprétation continue assez éloignée de la réalité.
Prenons l'exemple du modèle logistique de Verhulst défini dans le chapitre 1 :  .
.
La manipulation décrite plus haut amène à considérer l'équation différentielle  . Or, en faisant le changement de fonction
. Or, en faisant le changement de fonction  (légitime car avec la condition initiale, on est assuré que
(légitime car avec la condition initiale, on est assuré que  ne s'annule pas sur
ne s'annule pas sur  ), on est ramené à l'équation linéaire
), on est ramené à l'équation linéaire  , que l'on sait résoudre explicitement, et qui nous conduit à la solution suivante en
, que l'on sait résoudre explicitement, et qui nous conduit à la solution suivante en  :
:  .
.
Où est le problème ? Eh bien, il réside dans le fait que, quelque soit  , quelque soit
, quelque soit  , on a
, on a  . Donc ce système continu tend vers un état de stabilité, qui, si l'on revient au modèle initial, représente la saturation de la population. Choisissons par exemple
. Donc ce système continu tend vers un état de stabilité, qui, si l'on revient au modèle initial, représente la saturation de la population. Choisissons par exemple  . Si l'on se reporte à l'appendice du chapitre 1, on s'aperçoit que le modèle logistique discret correspondant à ce paramètre a le même comportement que l'itérateur quadratique
. Si l'on se reporte à l'appendice du chapitre 1, on s'aperçoit que le modèle logistique discret correspondant à ce paramètre a le même comportement que l'itérateur quadratique  , qui est complètement chaotique !
, qui est complètement chaotique !
Ceci montre bien l'invalidité de la démarche de passage au modèle continu dans ce cas.
D ] Des attracteurs étranges pour des systèmes continus
Ce paragraphe va permettre de visualiser des attracteurs de systèmes dynamiques continus. Les systèmes dynamiques continus sont des équations ou des systèmes d'équations différentielles. La donnée d'une condition initiale définit une unique solution. Cette solution, dans les exemples que nous allons voir, est une courbe de l'espace. Nous allons mettre en évidence des attracteurs étranges, comme des "objets" de l'espace qu'une telle courbe approche de plus en plus près, jusqu'à en donner une idée de la forme, au même titre qu'une orbite pour un système discret permettait de voir une esquisse de l'attracteur.
On retrouve les mêmes phénomènes que dans le domaine discret : des points fixes (ce seront ici des courbes périodiques), des cycles attractifs, le chaos (c'est là qu'on verra vraiment les attracteurs étranges), et lorsqu'on se ramène à l'étude discrète d'une variable (par exemple l'abscisse de tous les points consécutifs où la solution traverse tel ou tel plan fixe), on retrouve un diagramme de Feigenbaum, avec ses bifurcations, un point de Feigenbaum et bien sûr la constante de Feigenbaum.
1) L'attracteur de Rössler
L'attracteur de Rössler est l'attracteur du système dynamique continu caractérisé par le système différentiel  , pour lequel Rössler a proposé
, pour lequel Rössler a proposé  . Dans la suite, nous donnerons à
. Dans la suite, nous donnerons à  ces valeurs, mais nous ferons éventuellement varier
ces valeurs, mais nous ferons éventuellement varier  . Comme expliqué plus haut, chaque choix d'une condition initiale donnée par un vecteur
. Comme expliqué plus haut, chaque choix d'une condition initiale donnée par un vecteur  nous fournit une solution du système différentiel, qui correspond à ce qu'on avait appelé une orbite dans le cas discret.
nous fournit une solution du système différentiel, qui correspond à ce qu'on avait appelé une orbite dans le cas discret.
La commande a) dans la feuille de travail MAPLE permet de visualiser l'attracteur de Rössler pour les paramètres  . On a pris les conditions initiales
. On a pris les conditions initiales  , mais pour mieux voir l'attracteur, il faut éliminer le début de la courbe, puisque si attracteur il y a, la courbe doit s'en approcher de plus en plus, mais à la limite seulement. D'où la commande b), où on considère l'intervalle de temps
, mais pour mieux voir l'attracteur, il faut éliminer le début de la courbe, puisque si attracteur il y a, la courbe doit s'en approcher de plus en plus, mais à la limite seulement. D'où la commande b), où on considère l'intervalle de temps  .
.
La commande c) permet de voir comment l'attracteur se remplit davantage, en agrandissant l'intervalle de temps.
Puis la commande d) fait un tracé "impressionniste" de l'attracteur, en ne construisant que les points calculés par MAPLE.
En fait, toute solution dont le point initial est dans le bassin d'attraction de l'attracteur se comporte de la même manière : la courbe s'enroule en s'éloignant du centre, puis, lorsqu'elle est suffisamment excentré, fait un bond semblable à un geyser vers le haut, prenant ainsi une altitude d'autant plus élevée qu'elle s'était excentrée, et retombe plus près du centre, pour recommencer le cycle, qui n'en est pas vraiment un, car sinon on ne verrait qu'un seul arc jaillissant vers le haut. On peut pour une fois mettre à profit la lenteur de la machine pour voir comment cela se passe en paramétrant la couleur de la courbe en fonction du temps : c'est la commande e).
L'attracteur de Rössler ressemble donc, pour ce choix des paramètres, à une espèce de coquillage, que l'on perçoit comme une surface bien lisse. Le fait que cet objet soit un attracteur semble acceptable, puisqu'en changeant les conditions initiales, on obtient le même attracteur : en effet, en exécutant la commande f), on obtient un dessin tout à fait analogue, même s'il est intéressant de constater des différences dans les moments où telle ou telle partie de l'attracteur est dessinée. Pour la même raison, la propriété de mélange semble remplie.
Par contre, la structure fractale de cet attracteur n'est, elle, pas du tout évidente. Pourtant, on peut la prévoir en pensant au théorème de Cauchy-Lipschitz, qui affirme que par un point donné de l'espace, il ne passe qu'une solution et une seule d'un système différentiel comme celui de Rössler. Si donc l'attracteur était une surface, au sens usuel du terme, les solutions s'entrecroiseraient à loisir, ce qui est interdit. On en conclut que l'attracteur de Rössler est formé d'une infinie superposition de feuilles distinctes, sans intersection les unes avec les autres. On a en fait ce qu'on appelle un ensemble de Cantor de feuilles. On voit donc une surface, mais c'est en fait un très mince millefeuille. D'ailleurs, la dimension fractale de l'attracteur de Rössler est de très peu supérieure à celle d'une surface plane : elle est estimée entre  et
et  .
.
Pour la sensibilité aux conditions initiales, on peut, comme dans le cas de l'attracteur de Hénon, s'intéresser à la corrélation entre les abscisses (par exemple) des points courants de deux solutions correspondant à des conditions initiales proches. Le résultat de sensibilité-Rossler est moins spectaculaire que dans le cas de sensibilité_hénon, mais reste néanmoins visible. Cela tient au fait que la résolution du système différentiel se fait de façon numérique, explicitement avec la méthode de Runge-Kutta d'ordre 4-5, qui est une méthode itérative génératrice d'erreurs cumulées, et que l'on ne peut par conséquent demander une application de cette méthode sur un intervalle trop grand, car l'on risque de voir le phénomène à observer masqué par les erreurs de calcul. On se limite donc à 500 points environ, au lieu de 2000 ou 3000 pour sensibilité_hénon.
Il va sans dire que l'on peut construire des diagrammes de Feigenbaum, dans lesquels réapparaît la constante de Feigenbaum, (on peut par exemple, pour chaque paramètre  , considérer la suite des minima relatifs des abscisses lorsque le point mobile parcourt une solution donnée). Mais une procédure permettant la construction fiable d'un tel diagramme en MAPLE prendrait un temps prohibitif. On se contentera donc de vérifier à l'aide des commandes proposées que, pour certaines valeurs de
, considérer la suite des minima relatifs des abscisses lorsque le point mobile parcourt une solution donnée). Mais une procédure permettant la construction fiable d'un tel diagramme en MAPLE prendrait un temps prohibitif. On se contentera donc de vérifier à l'aide des commandes proposées que, pour certaines valeurs de  , on obtient bien une courbe périodique comme attracteur (en revenant à l'exemple ci-dessus de diagramme de Feigenbaum, le nombre de points de cette courbe où la fonction
, on obtient bien une courbe périodique comme attracteur (en revenant à l'exemple ci-dessus de diagramme de Feigenbaum, le nombre de points de cette courbe où la fonction  atteint un minimum relatif donne alors la période du cycle attractif correspondant).
atteint un minimum relatif donne alors la période du cycle attractif correspondant).
2) L'attracteur de Lorenz
C'est l'exemple le plus connu d'attracteur étrange. Il possède l'intérêt historique d'être l'attracteur correspondant à un système d'équations différentielles proposé par le météorologue Lorenz comme un modèle simplifié du déplacement des masses d'air dans l'atmosphère consécutivement à des variations de leur température.
Il s'agit du système différentiel 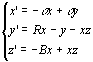 , pour lequel Lorenz a posé
, pour lequel Lorenz a posé 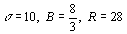 .
.
La première commande MAPLE propose une vue globale de l'attracteur de Lorenz pour ces paramètres, et pour un choix judicieux des conditions initiales. L'attracteur a la forme d'un papillon en vol, pour lequel les deux "yeux" des ailes seraient remplacés par des vides.
Pour mieux voir comment l'attracteur est décrit, la deuxième commande propose une restriction de l'intervalle du temps, associée à une coloration elle aussi dépendante du temps la courbe est décrite du plus clair au plus sombre).
On constate que le point courant arrive de l'extérieur de l'aile gauche, passe en brun clair sur l'intérieur de l'aile droite, y décrit deux boucles vers l'extérieur, puis passe en vert vers l'aile gauche, où il décrit une boucle, repasse en bleu cyan sur l'aile droite, où il décrit encore une boucle, pour repasser enfin sur l'aile gauche, où il décrit quatre boucles, avant de retourner en magenta foncé sur l'aile droite, etc...
On a donc quelque chose de comparable à la dynamique de l'attracteur de Rössler, puisque le point courant tourne autour du "centre" d'une aile, vers l'extérieur, avant de partir vers l'autre aile, et ainsi de suite. Sur le petit intervalle de temps précédent, on s'aperçoit déjà que le nombre de tours effectué sur chaque aile avant de la quitter semble aléatoire. En fait, on pense qu'il existe un entier  , tel que pour toute suite d'entiers appartenant à l'intervalle
, tel que pour toute suite d'entiers appartenant à l'intervalle  , il existe une solution incluse dans l'attracteur de Lorenz pour laquelle la suite des nombres des boucles effectuées aux visites consécutives de chaque aile coïncide avec la suite donnée.
, il existe une solution incluse dans l'attracteur de Lorenz pour laquelle la suite des nombres des boucles effectuées aux visites consécutives de chaque aile coïncide avec la suite donnée.
Quant à la structure fractale de l'attracteur de Lorenz, elle procède du même argument que pour l'attracteur de Rössler. Et il y a de nouveau existence de solutions périodiques attractives, comme le montre la troisième commande, et il arrive même qu'il y ait coexistence, pour certains paramètres, de solutions périodiques attractives et d'attracteurs chaotiques étranges...
E ] La reconstruction des attracteurs étranges
Dans la pratique de l'étude des systèmes dynamiques réels, on ne possède malheureusement pas d'équation différentielle ou de fonction d'itération explicite permettant de décrire le phénomène observé. Au contraire, on ne connaît souvent qu'une liste de données expérimentales, nécessairement discrètes, et il s'agit avec cela de reconstruire le système dynamique sous-jacent. On s'en doute, ceci est une entreprise difficile et bien souvent hasardeuse.
La première approche est de voir s'il existe une fonction donnant la  -ième observation en fonction de la précédente, ou d'un certain nombre des précédentes. Ceci est réalisable informatiquement, et donne des résultats intéressants.
-ième observation en fonction de la précédente, ou d'un certain nombre des précédentes. Ceci est réalisable informatiquement, et donne des résultats intéressants.
Lorsqu'on applique cette approche, par la procédure approche1, à une liste de valeurs aléatoires créée grâce à la procédure rand de MAPLE, on obtient effectivement une distribution bien répartie dans le carré des possibilités. Mais lorsqu'on crée cette liste par application de l'itérateur quadratique  , on obtient exactement la parabole représentative de cette fonction, ce qui est prévisible, puisque d'une part cet itérateur a un comportement chaotique, ce qui fait que les valeurs de la liste créée par crée_liste se répartissent dans
, on obtient exactement la parabole représentative de cette fonction, ce qui est prévisible, puisque d'une part cet itérateur a un comportement chaotique, ce qui fait que les valeurs de la liste créée par crée_liste se répartissent dans  , et que d'autre part chaque point construit dans approche1 est un point de la parabole.
, et que d'autre part chaque point construit dans approche1 est un point de la parabole.
Plus surprenante par contre est l'apparition, lorsqu'on crée une liste de données avec la suite des abscisses des itérés par la fonction de Hénon, d'un graphe ayant la forme générale de l'attracteur de Hénon lui-même !
Encouragés par ce succès, nous allons essayer d'appliquer la même approche à l'attracteur de Rössler. Pour cela, nous allons choisir un intervalle de temps séparant deux collectes de données consécutives. Cet intervalle étant ici , on considère la liste de données fournie par le calcul des cotes des points d'une solution du bassin d'attraction, pris en des temps successifs séparés du délai choisi. Le résultat est cette fois-ci peu interprétable. On pouvait s'y attendre, du fait que l'attracteur de Rössler n'est pas plane.
, on considère la liste de données fournie par le calcul des cotes des points d'une solution du bassin d'attraction, pris en des temps successifs séparés du délai choisi. Le résultat est cette fois-ci peu interprétable. On pouvait s'y attendre, du fait que l'attracteur de Rössler n'est pas plane.
Dans un cas comme celui-ci, on utilise une deuxième approche, consistant à choisir un délai  égal à un multiple de
égal à un multiple de  , puis à construire une suite de points de la façon suivante (on aurait aussi pu prendre l'abscisse ou l'ordonnée):
, puis à construire une suite de points de la façon suivante (on aurait aussi pu prendre l'abscisse ou l'ordonnée):

Cette approche est matérialisée par une suite de commandes exploitant cette méthode, appelée méthode des phases. Les choix de l'intervalle de temps et du délai influencent fortement le résultat. Il semble que  soit une bonne valeur, et on a pris
soit une bonne valeur, et on a pris  pour obtenir un lissé suffisant du résultat. La méthode de résolution numérique du système différentiel de Rössler a été également modifiée : une méthode classique type Euler ou Heun est moins gourmande en calculs, et semble suffisante pour le résultat escompté.
pour obtenir un lissé suffisant du résultat. La méthode de résolution numérique du système différentiel de Rössler a été également modifiée : une méthode classique type Euler ou Heun est moins gourmande en calculs, et semble suffisante pour le résultat escompté.
Ce qu'on obtient ressemble effectivement à l'attracteur de Rössler, du moins dans sa forme générale. Les différences essentielles résident en une partie centrale pleine, et une partie médiane vide. En fait, si l'on augmente beaucoup le compteur k (par exemple à 5000), on constate que la partie médiane se remplit peu à peu.
Malgré ses limites, dues essentiellement à la puissance de nos machines, ce programme permet tout de même de montrer la pertinence de la méthode des phases. D'ailleurs, le résultat est encore plus probant si l'on applique la méthode à l'attracteur de Lorenz.
A noter que les diagrammes des phases obtenus ne sont pas des copies exactes des attracteurs qu'ils sont censés reconstruire, mais seulement des objets géométriques ayant sensiblement les mêmes propriétés. De plus, il faut choisir avec soin le délai pour reconnaître l'attracteur cherché, ce qui laisse encore un espace à l'expérimentation lorsqu'on applique la méthode à une suite de données quelconque...
Chapitre précédent Sommaire Chapitre suivant
 de l'espace est un attracteur étrange et chaotique pour une transformation
de l'espace est un attracteur étrange et chaotique pour une transformation  de l'espace s'il existe un voisinage
de l'espace s'il existe un voisinage  de
de  (c'est à dire que pour tout point de
(c'est à dire que pour tout point de  il existe une boule contenant ce point et contenue dans
il existe une boule contenant ce point et contenue dans  ) vérifiant les propriétés suivantes :
) vérifiant les propriétés suivantes :
 . (attention, les attracteurs pour les autres valeurs de
. (attention, les attracteurs pour les autres valeurs de  sont soit périodiques, donc ne vérifient pas la propriété 2), soit égaux à une réunion d'intervalles, et donc ne vérifient pas 3))
sont soit périodiques, donc ne vérifient pas la propriété 2), soit égaux à une réunion d'intervalles, et donc ne vérifient pas 3))
 .
.
 est en dehors de l'attracteur. Son orbite approxime néanmoins l'attracteur : on peut donc le considérer comme un point d'une zone de capture éventuelle. Et en effet, Hénon a proposé comme zone de capture
est en dehors de l'attracteur. Son orbite approxime néanmoins l'attracteur : on peut donc le considérer comme un point d'une zone de capture éventuelle. Et en effet, Hénon a proposé comme zone de capture  un quadrilatère que l'on peut visualiser grâce à la commande display qui suit. L'attracteur a été réesquissé pour montrer son inclusion dans cette zone. On constate alors que des points très proches de l'attracteur sont exclus de ce quadrilatère. En prenant le point (1.292;0), on s'aperçoit en effet que son orbite s'éloigne indéfiniment. Avec hénon(1.292,0,20,1.4,.3), on obtient des coordonnées trop grandes en valeur absolue lors des calculs, et un message d'erreur s'affiche.
un quadrilatère que l'on peut visualiser grâce à la commande display qui suit. L'attracteur a été réesquissé pour montrer son inclusion dans cette zone. On constate alors que des points très proches de l'attracteur sont exclus de ce quadrilatère. En prenant le point (1.292;0), on s'aperçoit en effet que son orbite s'éloigne indéfiniment. Avec hénon(1.292,0,20,1.4,.3), on obtient des coordonnées trop grandes en valeur absolue lors des calculs, et un message d'erreur s'affiche.
 qu'il n'a pas une forme évidente a priori.
qu'il n'a pas une forme évidente a priori.
 a pour jacobien en
a pour jacobien en  le déterminant
le déterminant  . Il en résulte que si
. Il en résulte que si  , on peut considérer que chaque application à un sous-ensemble du plan de la transformation de Hénon réduit son aire du facteur
, on peut considérer que chaque application à un sous-ensemble du plan de la transformation de Hénon réduit son aire du facteur  . Dans le cas
. Dans le cas  , et sachant que l'on peut aussi considérer l'attracteur de Hénon comme l'attracteur d'un IFS, on en déduit que si l'on part initialement d'une forme géométrique quelconque, par exemple un triangle, l'attracteur aura à la limite une aire nulle.
, et sachant que l'on peut aussi considérer l'attracteur de Hénon comme l'attracteur d'un IFS, on en déduit que si l'on part initialement d'une forme géométrique quelconque, par exemple un triangle, l'attracteur aura à la limite une aire nulle.
 .
.
 , où
, où  est la suite des abscisses des itérés par la transformation de Hénon d'un certain point, tandis que
est la suite des abscisses des itérés par la transformation de Hénon d'un certain point, tandis que  est la suite des abscisses des itérés d'un autre point, pris très proche du premier (on pourrait naturellement faire la même chose sur les ordonnées).
est la suite des abscisses des itérés d'un autre point, pris très proche du premier (on pourrait naturellement faire la même chose sur les ordonnées).
 )).
)).
 .
.
 , et on va faire varier
, et on va faire varier  pour obtenir un diagramme de Feigenbaum. Pour pouvoir facilement le comparer avec celui de l'
pour obtenir un diagramme de Feigenbaum. Pour pouvoir facilement le comparer avec celui de l' , il semble y avoir coexistence de plusieurs attracteurs différents. C'est pour permettre de voir cela que la procédure est si complexe : il y a essai de vingt points initiaux différents pour chaque paramètre, par balayage sur l'ordonnée autour de
, il semble y avoir coexistence de plusieurs attracteurs différents. C'est pour permettre de voir cela que la procédure est si complexe : il y a essai de vingt points initiaux différents pour chaque paramètre, par balayage sur l'ordonnée autour de  ; s'il y a dépassement dans les calculs, cela signifie que le point n'est dans aucun bassin d'attraction. Sinon, on ajoute son orbite à l'ensemble des points à dessiner. Ceci est nécessaire dans la mesure où on ignore comment est situé le bassin d'attraction de chaque attracteur. Pour limiter le cardinal de l'ensemble des points à tracer, on travaille modulo
; s'il y a dépassement dans les calculs, cela signifie que le point n'est dans aucun bassin d'attraction. Sinon, on ajoute son orbite à l'ensemble des points à dessiner. Ceci est nécessaire dans la mesure où on ignore comment est situé le bassin d'attraction de chaque attracteur. Pour limiter le cardinal de l'ensemble des points à tracer, on travaille modulo  .
.
 d'un sous-ensemble
d'un sous-ensemble  d'un espace métrique dans lui-même, et la "formule"
d'un espace métrique dans lui-même, et la "formule"  .
.
 . En modifiant quelque peu les notations, on a donc
. En modifiant quelque peu les notations, on a donc  , dont la première égalité peut s'écrire
, dont la première égalité peut s'écrire  . Dans ce processus dynamique, on passe d'un itéré au suivant en incrémentant
. Dans ce processus dynamique, on passe d'un itéré au suivant en incrémentant  de 1 à chaque fois. Imaginons maintenant qu'on l'incrémente d'une fraction seulement de 1, soit
de 1 à chaque fois. Imaginons maintenant qu'on l'incrémente d'une fraction seulement de 1, soit  . On obtient
. On obtient  . Lorsque
. Lorsque  , tout élève de terminale dit que
, tout élève de terminale dit que  . Cette audacieuse manoeuvre doit sa réussite au fait que l'on considère dorénavant
. Cette audacieuse manoeuvre doit sa réussite au fait que l'on considère dorénavant  comme une fonction d'une variable
comme une fonction d'une variable 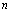 , et que l'on étudie précisément cette fonction en un point qui s'appelle aussi
, et que l'on étudie précisément cette fonction en un point qui s'appelle aussi  ne dépendait que du point
ne dépendait que du point  , lui, dépend du point
, lui, dépend du point  et de la fonction
et de la fonction 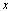 . On est donc amené à écrire
. On est donc amené à écrire  , ou encore, en posant
, ou encore, en posant  :
:  .
.
 .
.
 , alors le système continu correspondant sera de la forme
, alors le système continu correspondant sera de la forme  , ce qui est la forme habituelle d'une équation différentielle ordinaire du premier ordre.
, ce qui est la forme habituelle d'une équation différentielle ordinaire du premier ordre.
 , on obtient un système d'équations différentielles
, on obtient un système d'équations différentielles  , et ainsi de suite...
, et ainsi de suite...
 .
.
 . Or, en faisant le changement de fonction
. Or, en faisant le changement de fonction  (légitime car avec la condition initiale, on est assuré que
(légitime car avec la condition initiale, on est assuré que  ne s'annule pas sur
ne s'annule pas sur  ), on est ramené à l'équation linéaire
), on est ramené à l'équation linéaire  , que l'on sait résoudre explicitement, et qui nous conduit à la solution suivante en
, que l'on sait résoudre explicitement, et qui nous conduit à la solution suivante en  .
.
 , quelque soit
, quelque soit  , on a
, on a  . Donc ce système continu tend vers un état de stabilité, qui, si l'on revient au modèle initial, représente la saturation de la population. Choisissons par exemple
. Donc ce système continu tend vers un état de stabilité, qui, si l'on revient au modèle initial, représente la saturation de la population. Choisissons par exemple  . Si l'on se reporte à l'appendice du
. Si l'on se reporte à l'appendice du  , qui est complètement chaotique !
, qui est complètement chaotique !
 , pour lequel Rössler a proposé
, pour lequel Rössler a proposé  . Dans la suite, nous donnerons à
. Dans la suite, nous donnerons à  ces valeurs, mais nous ferons éventuellement varier
ces valeurs, mais nous ferons éventuellement varier  . Comme expliqué plus haut, chaque choix d'une condition initiale donnée par un vecteur
. Comme expliqué plus haut, chaque choix d'une condition initiale donnée par un vecteur  nous fournit une solution du système différentiel, qui correspond à ce qu'on avait appelé une orbite dans le cas discret.
nous fournit une solution du système différentiel, qui correspond à ce qu'on avait appelé une orbite dans le cas discret.
 , mais pour mieux voir l'attracteur, il faut éliminer le début de la courbe, puisque si attracteur il y a, la courbe doit s'en approcher de plus en plus, mais à la limite seulement. D'où la commande b), où on considère l'intervalle de temps
, mais pour mieux voir l'attracteur, il faut éliminer le début de la courbe, puisque si attracteur il y a, la courbe doit s'en approcher de plus en plus, mais à la limite seulement. D'où la commande b), où on considère l'intervalle de temps  .
. et
et  .
.
 atteint un minimum relatif donne alors la période du cycle attractif correspondant).
atteint un minimum relatif donne alors la période du cycle attractif correspondant).
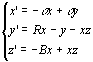 , pour lequel Lorenz a posé
, pour lequel Lorenz a posé 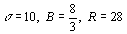 .
. , tel que pour toute suite d'entiers appartenant à l'intervalle
, tel que pour toute suite d'entiers appartenant à l'intervalle  , il existe une solution incluse dans l'attracteur de Lorenz pour laquelle la suite des nombres des boucles effectuées aux visites consécutives de chaque aile coïncide avec la suite donnée.
, il existe une solution incluse dans l'attracteur de Lorenz pour laquelle la suite des nombres des boucles effectuées aux visites consécutives de chaque aile coïncide avec la suite donnée.
 -ième observation en fonction de la précédente, ou d'un certain nombre des précédentes. Ceci est réalisable informatiquement, et donne des résultats intéressants.
-ième observation en fonction de la précédente, ou d'un certain nombre des précédentes. Ceci est réalisable informatiquement, et donne des résultats intéressants.
 , on obtient exactement la parabole représentative de cette fonction, ce qui est prévisible, puisque d'une part cet itérateur a un comportement chaotique, ce qui fait que les valeurs de la liste créée par crée_liste se répartissent dans
, on obtient exactement la parabole représentative de cette fonction, ce qui est prévisible, puisque d'une part cet itérateur a un comportement chaotique, ce qui fait que les valeurs de la liste créée par crée_liste se répartissent dans  , et que d'autre part chaque point construit dans approche1 est un point de la parabole.
, et que d'autre part chaque point construit dans approche1 est un point de la parabole.
 , on considère la liste de données fournie par le calcul des cotes des points d'une solution du bassin d'attraction, pris en des temps successifs séparés du délai choisi. Le résultat est cette fois-ci peu interprétable. On pouvait s'y attendre, du fait que l'attracteur de Rössler n'est pas plane.
, on considère la liste de données fournie par le calcul des cotes des points d'une solution du bassin d'attraction, pris en des temps successifs séparés du délai choisi. Le résultat est cette fois-ci peu interprétable. On pouvait s'y attendre, du fait que l'attracteur de Rössler n'est pas plane.
 égal à un multiple de
égal à un multiple de  , puis à construire une suite de points de la façon suivante (on aurait aussi pu prendre l'abscisse ou l'ordonnée):
, puis à construire une suite de points de la façon suivante (on aurait aussi pu prendre l'abscisse ou l'ordonnée):

 soit une bonne valeur, et on a pris
soit une bonne valeur, et on a pris  pour obtenir un lissé suffisant du résultat. La méthode de résolution numérique du système différentiel de Rössler a été également modifiée : une méthode classique type Euler ou Heun est moins gourmande en calculs, et semble suffisante pour le résultat escompté.
pour obtenir un lissé suffisant du résultat. La méthode de résolution numérique du système différentiel de Rössler a été également modifiée : une méthode classique type Euler ou Heun est moins gourmande en calculs, et semble suffisante pour le résultat escompté.