 de l'espace
de l'espace  , une fonction
, une fonction  de
de  dans
dans  telle que
telle que 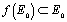 , et on crée le système dynamique discret défini par
, et on crée le système dynamique discret défini par  .
.
CHAPITRE 3 :LES FRACTALS
FICHIER MAPLE CORRESPONDANT : FRACTAL.MWS
I. Approche qualitative
A ] Introduction
La notion de fractal recouvre des objets géométriques - courbes, surfaces, volumes, voire objets de dimension supérieure - dont il est difficile de donner une définition générale. On se contentera d'en dégager les propriétés caractéristiques et les éléments quantifiables.
Dans ce chapitre, on va décrire et comparer qualitativement quelques systèmes dynamiques aboutissant à des fractals.
C'est Mandelbrot qui a le premier montré au public l'existence des fractals. Dans son livre de 1982, The Fractal Geometry of Nature, il montre toute la beauté et le fascinant mystère de ces objets géométriques, utilisant notamment des images obtenues par ordinateur. Mais surtout, il montre que nous sommes en fait entourés "naturellement" d'objets fractals.
En effet, la caractéristique visuelle essentielle de ces objets est que, naïvement, on peut en couper un morceau quelconque, agrandir ce morceau à une échelle telle qu'il ait la taille de l'objet initial, et on retrouve alors une quasi-copie de cet objet initial. De plus, ce processus de coupure-agrandissement peut se répéter indéfiniment...
Cette caractéristique s'appelle l'auto-similitude.
Vu dans ce sens, des exemples d'objets fractals dans la nature sont faciles à trouver. Citons entre autres: la ligne qui forme la côte d'un pays maritime, les nuages (ou les choux-fleurs!), les fougères, les flammes, la surface d'un torrent, etc...
Ces objets fractals naturels sont dits non-déterministes, car le processus dynamique qui permet leur création varie lui-même avec le temps de façon aléatoire: penser à la formation d'un nuage, qui dépend de la pression, de la température, du vent, toutes données qui ne sont pas fixes pendant le processus.
On peut néanmoins essayer de modéliser des systèmes dynamiques permettant d'aboutir à des objets fractals, sous la forme suivante:
a) On se donne un objet géométrique initial  de l'espace
de l'espace  , une fonction
, une fonction  de
de  dans
dans  telle que
telle que 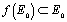 , et on crée le système dynamique discret défini par
, et on crée le système dynamique discret défini par  .
.
b) Sous certaines conditions, la suite d'objets géométriques  "tend" vers une limite, qui est souvent un objet fractal.
"tend" vers une limite, qui est souvent un objet fractal.
Naturellement, il existe un cadre mathématique rigoureux dans lequel les conditions évoquées et le verbe tendre ont une définition précise. En particulier, les objets  sont tous des compacts de
sont tous des compacts de  , c'est à dire des sous-ensembles bornés (qu'on peut inclure dans un segment (si
, c'est à dire des sous-ensembles bornés (qu'on peut inclure dans un segment (si  est une droite), un disque (si
est une droite), un disque (si  est un plan) ou une boule (si
est un plan) ou une boule (si  est l'espace à trois dimensions)) et fermés (toute suite convergente de
est l'espace à trois dimensions)) et fermés (toute suite convergente de  a sa limite dans
a sa limite dans  ) ; on se place alors dans l'espace métrique des compacts, muni de la distance de Hausdorff, dont on montre qu'il est complet lorsqu'il s'agit de compacts du plan et de l'espace, et on vérifie que
) ; on se place alors dans l'espace métrique des compacts, muni de la distance de Hausdorff, dont on montre qu'il est complet lorsqu'il s'agit de compacts du plan et de l'espace, et on vérifie que  est un opérateur de Hutchinson, c'est à dire une application contractante de l'espace des compacts dans lui-même pour cette distance. Il ne reste plus alors qu'à appliquer le théorème du point fixe. A noter que tout opérateur sur les compacts formé avec un système de transformations affines de déterminant strictement inférieur à 1 est un opérateur de Hutchinson : c'est le cas de tous les systèmes dynamiques définis ci-dessous.
est un opérateur de Hutchinson, c'est à dire une application contractante de l'espace des compacts dans lui-même pour cette distance. Il ne reste plus alors qu'à appliquer le théorème du point fixe. A noter que tout opérateur sur les compacts formé avec un système de transformations affines de déterminant strictement inférieur à 1 est un opérateur de Hutchinson : c'est le cas de tous les systèmes dynamiques définis ci-dessous.
Des systèmes dynamiques de ce type sont dits déterministes, et appelés IFS (deteministic iterated function systems).
Précisons que la limite de l'IFS s'appelle l'attracteur de l'IFS. On peut montrer que sous les conditions évoquées plus haut, cet attracteur ne dépend pas de la forme de l'objet géométrique initial. Dans les exemples suivants, l'objet initial est un triangle, mais il pourrait être n'importe quoi, comme on le verra dans l'exemple de l'ensemble de Cantor.
B ] Un exemple de fractal obtenu par IFS sur une droite: l'ensemble de Cantor
Dans cet exemple,  est la droite des nombres réels,
est la droite des nombres réels,  , et
, et  , avec
, avec
 .
.
Géométriquement, on part du segment  , dont on enlève le tiers médian. On obtient ainsi deux segments disjoints (voir Cantor(1)), auxquels on applique séparément le même procédé, et ainsi de suite. A chaque étape, on garde la réunion des segments qui restent après avoir enlevé de chacun des segments de l'étape précédente le tiers médian.
, dont on enlève le tiers médian. On obtient ainsi deux segments disjoints (voir Cantor(1)), auxquels on applique séparément le même procédé, et ainsi de suite. A chaque étape, on garde la réunion des segments qui restent après avoir enlevé de chacun des segments de l'étape précédente le tiers médian.
L'ensemble de Cantor est l'ensemble de points que l'on obtient à la limite.
La fonction Cantor permet de visualiser le processus. Naturellement, le coût de l'algorithme d'affichage est prohibitif, puisque le nombre de segments à tracer double à chaque itération. On se contentera d'appeler Cantor pour de petites valeurs de n, ce qui n'est pas vraiment grave, puisqu'on se rend compte que les capacités d'affichage de l'écran et notre propre vue rendent rapidement les figures successives indiscernables.
Un zoom de l'écran permet de discerner un ou deux crans plus loin, et surtout, ne montrant qu'une partie de la figure à la fois, permet de bien illustrer la propriété d'auto-similitude évoquée plus haut comme une caractéristique des objets fractals.
L'ensemble de Cantor possède des propriétés intéressantes, toutes démontrables en taupe (=prépa ;-). Citons:
1) Mathématiquement, il peut aussi être défini comme l'ensemble des nombres de  dont le développement du type
dont le développement du type  en base 3 ne contient aucun chiffre 1. En particulier, il contient bien d'autres points que les bornes des petits intervalles formant la figure à chaque itération de l'IFS.
en base 3 ne contient aucun chiffre 1. En particulier, il contient bien d'autres points que les bornes des petits intervalles formant la figure à chaque itération de l'IFS.
2) Il est de probabilité nulle dans  .
.
3) Il est non dénombrable.
4) Il ne contient aucun segment.
5) Aucun point n'est isolé: pour chaque point de l'ensemble de Cantor, chaque sous-intervalle de  qui le contient en contient au moins un autre, et donc une infinité.
qui le contient en contient au moins un autre, et donc une infinité.
C ] Des exemples de fractals dans le plan:
Dans cette partie, il s'agit surtout de comparer les comportements de certains IFS célèbres, en essayant de pousser le plus loin possible le nombre d'itérations sur l'ordinateur, et en jouant éventuellement avec le zoom.
Attention toutefois, l'algorithme utilisé est de complexité exponentielle, ce qui fait qu'à chaque itération supplémentaire, on multiplie le temps de traitement par un facteur égal au nombre de transformations qui constituent l'IFS. Augmentez le nombre n à chaque appel de IFS pour un IFS donné, et arrêtez-vous quand le traitement dépasse quelques minutes.
Le tamis de Sierpinski est l'un des attracteurs les plus célèbres. Il sert de modèle simple pour l'étude de nombreux phénomènes reliés aux fractals et au chaos. Par exemple, lorsqu'on colorie dans le triangle de Pascal les coefficients binômiaux pairs, on voit apparaître un tamis de Sierpinski.
L'arbre de Noël est amusant, la convergence vers l'attracteur est très rapide.
Le labyrinthe de Sierpinski est un attracteur dans lequel on peut voir des produits cartésiens d'ensembles de Cantor.
Le rameau et le cristal semblent avoir une convergence plus lente, tandis que le mécano a une convergence très rapide, qui permet d'observer la disparition assez rapide des formes triangulaires. Heureusement, car la complexité de l'algorithme est en  !
!
Le feu est une découverte personnelle, vous pouvez vous aussi essayer vos propres variantes.
L'arbre parle de lui-même, bien qu'il ne croisse pas trop vite.
Les deux versions d'ensemble de Cantor montrent que si l'on plonge la droite des réels dans le plan, l'ensemble de Cantor est un attracteur plane comme les autres.
Dans la première version, on a triché, puisque les deux transformations utilisées sont des projections sur la droite des réels, et par conséquent, dès la seconde itération, on travaille avec des segments comme dans Cantor.
Par contre, dans la seconde, on a de véritables transformations planes, et pourtant, au bout d'un petit nombre d'itérations, on ne voit plus que des segments!
Jusqu'à présent, la vitesse de convergence vers l'attracteur était suffisamment rapide pour qu'on puisse parvenir jusqu'au point où deux itérations successives sont indiscernables à l'écran.
Il n'en est plus du tout de même pour la fougère de Barnsley. L'attracteur ressemble à s'y méprendre à une vraie fougère, mais il est difficile de s'en convaincre avec les premières itérations!
Mathématiquement, l'existence de cet attracteur est prouvé, mais on n'a aucune chance de voir quoi que ce soit avec l'IFS, dût-on attendre toute sa vie devant la machine la plus rapide existant actuellement! Pour s'en convaincre, il suffit de penser que si on obtient l'itéré numéro n en un jour, il faudra quatre jours pour obtenir le numéro suivant et plus d'un an pour avoir le numéro n+5, et encore cinq fois plus longtemps pour avoir le suivant.
On verra plus loin une élégante manière de tracer ce type d'attracteur à peu de frais. Pour le montrer de façon plus éclatante, on utilisera une fougère plus simple que la fougère de Barnsley, mais qui ne ressemble aux premiers stades de sa construction guère davantage à une fougère!
C ] Où le chaos nous vient en aide pour visualiser des attracteurs timides
L'idée de départ est simple: si comme figure de départ dans l'itération d'un IFS, on prend un simple point, les figures successives vont encore converger vers l'attracteur, car un point satisfait aux conditions évoquées plus haut.
Mais ce choix ne diminue pas la complexité de l'algorithme, parce qu'à chaque étape, le nombre de points à tracer croît encore de façon exponentielle.
Par contre, si l'on n'applique à chaque étape que l'une des transformations de l'IFS, la croissance va devenir linéaire, et on restera quand même assuré de ce que les points de la suite obtenue vont être de plus en plus proches de points appartenant à l'attracteur.
Seulement, on ne peut appliquer en général n'importe quelle transformation à chaque itération: la bonne stratégie consiste à la choisir au hasard, et en donnant à ces transformations des probabilités différentes d'être appliquées.
Il existe des règles d'estimation simples pour choisir des probabilités correctes, mais ensuite on peut encore améliorer ces choix en utilisant des méthodes plus fines, et en tenant compte de la résolution de l'écran.
L'orbite d'un point, construite ainsi de façon aléatoire adaptée, va se rapprocher de plus en plus de l'attracteur, et un nombre de points de l'ordre de dix à vingt mille donne, si les probabilités sont bien choisies, une excellente idée de l'attracteur. On dit d'une telle orbite qu'elle est ergodique, aussi la procédure s'appelle-t'elle IFS_ergodique.
IFS_ergodique est ce qu'on appelle une IFS non-déterministe.
En la testant avec les fougères, on voit apparaître les contours, certes encore flous, mais bien reconnaissables de ces plantes, et ceci avec un temps de calcul assez court. Par contre, avec mécano, par exemple, on perd plutôt en efficacité par rapport à l'IFS classique.
Avec le tamis de Sierpinski, les probabilités doivent évidemment être égales, et le résultat est probant. Il est intéressant de voir ce qu'on obtient avec d'autres probabilités.
Remarque:
La fonction choix_en_fonction_de, permettant de choisir la transformation à appliquer en fonction des probabilités fixées, utilise dans sa construction la fonction rand, qui est la fonction de MAPLE permettant la génération de nombres aléatoires. Une procédure comme choix_en_fonction_de est un exemple de ce qu'on appelle les méthodes de Monte Carlo.
Néanmoins, une fonction comme rand n'est pas vraiment aléatoire. Elle est pseudo-aléatoire, en ce sens qu'elle utilise un algorithme déterministe, qui est d'ailleurs en général la méthode de congruence linéaire (encore un système dynamique discret!).
Un moyen amusant de tester si un générateur de nombres aléatoires est efficace est de l'utiliser à la place de rand.
Par exemple, avec une autre méthode célèbre, comme la méthode du middle square generator, proposée par Von Neumann, on s'aperçoit qu'on n'obtient qu'une portion très limitée du tamis de Sierpinski, ce qui prouve l'invalidité de cette méthode.
De même, vu le comportement chaotique de l'itérateur quadratique étudié au chapitre 2, on pourrait être tenté de l'utiliser pour générer des nombres aléatoires. Mais là encore, le résultat obtenu sur le tamis de Sierpinski indique un comportement non aléatoire, ce qui prouve que chaotique et aléatoire ne sont pas synonymes!
Cette application originale des attracteurs d'IFS au test de l'efficacité d'un générateur de nombres aléatoires méritait d'être soulignée.
D ] Le flocon de Koch
On peut démontrer que, de façon surprenante, tous les points du tamis de Sierpinski peuvent être reliés en une courbe continue! Cette courbe n'est dérivable nulle part, cependant.
Un autre exemple fameux d'un "monstre mathématique" de ce type est la Courbe de Koch, qui présente par rapport a l'exemple précédent l'avantage de montrer visuellement - mais aussi sans trop d'efforts - que cet objet fractal est une courbe continue, mais dérivable en aucun point.
Fidèle à l'esprit de ce chapitre, on se contentera de visualiser le phénomène.
D'abord, la courbe de Koch est définie comme l'attracteur d'un IFS courbe_de_Koch , dont la structure est analogue à celle de IFS, à ceci près que l'objet initial est un segment, et que pour maintenir la continuité de la courbe polygonale obtenue à chaque itération, il importe de contrôler l'ordre dans lequel sont effectuées les quatre transformations de l'IFS.
On voit qu'au fur et à mesure que les itérations augmentent, la figure obtenue reste une courbe continue, mais qu'il y a de plus en plus de points anguleux, ces points anguleux restant définitivement sur la courbe après leur apparition.
A la limite, c'est-à-dire sur l'attracteur, tous les points sont anguleux, ce qui s'interprète par la non-dérivabilité de la courbe en tout point.
Lorsqu'on applique cet IFS aux trois côtés d'un triangle équilatéral initial, on obtient une courbe fermée, qu'on appelle le flocon de Koch (ou l'île de Koch si l'on se réfère plutôt à la surface qu'elle entoure).
La procédure flocon_de_Koch construit les premiers itérés menant au flocon, et la convergence est suffisamment rapide pour qu'on puisse voir l'allure de l'attracteur. Elle est définie en utilisant le corps de la procédure courbe_de_Koch et en recollant judicieusement trois copies de cette courbe.
On peut remarquer que le flocon de Koch a une longueur infinie (puisqu'à chaque étape on multiplie la longueur par  , alors que l'île de Koch a une aire finie (puisque si l'on appelle
, alors que l'île de Koch a une aire finie (puisque si l'on appelle 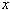 l'aire du triangle de départ, l'aire de l'île d'ordre
l'aire du triangle de départ, l'aire de l'île d'ordre  est égale à
est égale à  , qui est une série géométrique de limite
, qui est une série géométrique de limite  ), dans notre cas égale à
), dans notre cas égale à  .
.
Ce phénomène modélise bien le paradoxe célèbre, proposé par Mandelbrot pour introduire la notion de fractal, de la longueur infinie de la côte de la Grande-Bretagne, alors que la surface de ce pays est évidemment finie.
E ] Conclusion:
Ce chapitre a permis de présenter, et surtout de visualiser la notion d'objet fractal. Par simplicité, je me suis imposé deux limitations: la première est que je n'ai traité que de fractals dans le plan, alors qu'on peut parfaitement en définir dans l'espace.
La seconde est que j'ai choisi la présentation d'un fractal comme attracteur d'un IFS. C'est la plus commode pour l'écriture de programmes qui, en MAPLE (parce qu'il y a des graphiques en sortie), sont plus faciles à écrire car naturellement itératifs. De plus, cette approche permet de démontrer élégamment les phénomènes observés.
Mais il existe d'autres approches. Citons:
- L'approche par les L-systèmes , qui correspond au niveau programmation à une vision récursive arborescente à nombre de fils constant de l'IFS.
- L'approche par les automates cellulaires, qui correspond à une vision itérative, l'itération étant effectuée sur des tests de conditions, et non par des transformations géométriques.
Dans les deux cas, on peut évidemment reconstruire les attracteurs vus dans ce chapitre.
Je n'ai pas abordé le problème réciproque, à savoir: une figure du plan, fractale ou non, étant donnée, peut-on trouver un IFS dont l'attracteur soit ce fractal? Le problème est difficile, comme on peut se l'imaginer, et comme la complexité des transformations utilisées pour créer la fougère de Barnsley le montre bien...
Pourtant, c'est une vraie question, car certains fractals, comme les ensembles de Julia, que nous verrons au chapitre 6, apparaissent hors d'un contexte d'IFS, et il sera intéressant pour les construire efficacement de disposer d'un IFS qui les admette comme attracteur.
II. Approche quantitative
A ] Introduction
Dans ce chapitre, on va aborder la notion de dimension fractionnaire d'un objet géométrique, ou plutôt, on va discuter de plusieurs façons de définir cette notion.
Intuitivement, la dimension d'un objet géométrique est un entier correspondant au nombre de paramètres nécessaire pour le définir : par exemple, un point est de dimension nulle, un segment de dimension 1, un cube de dimension 3...
Cela correspond aussi aux unités nécessaires pour les quantifier : cm, cm2, cm3, etc...
C'est la définition de la dimension d'un espace affine que l'on rencontre en algèbre.
Par extension, une courbe est donc de dimension 1 (penser à l'unité nécessaire pour en donner la mesure), un disque de dimension 2, etc...C'est là que commence la difficulté !
En effet, que dire de la courbe  ? On définit alors la notion de dimension topologique : par exemple, une courbe est de dimension (topologique) 1 s'il existe une bijection continue d'un intervalle de
? On définit alors la notion de dimension topologique : par exemple, une courbe est de dimension (topologique) 1 s'il existe une bijection continue d'un intervalle de  sur la courbe (ou plutôt sur l'intervalle parcouru par son paramètre en représentation paramétrique), et dont la bijection réciproque est aussi continue. Une telle bijection s'appelle un homéomorphisme.
sur la courbe (ou plutôt sur l'intervalle parcouru par son paramètre en représentation paramétrique), et dont la bijection réciproque est aussi continue. Une telle bijection s'appelle un homéomorphisme.
Cette définition de la dimension d'un objet semble cependant restrictive, car elle ne s'applique qu'à des objets reconnus comme des courbes continues. Par exemple, elle ne s'applique pas a priori à l'ensemble de Cantor, ou au tamis de Sierpinski. Un exemple de définition plus générale est la notion de dimension topologique par recouvrement. En voici la définition dans le plan, pour des ensembles compacts, c'est-à-dire fermés et bornés:
Définitions préliminaires :
1) Un recouvrement fini d'un sous-ensemble compact  du plan est un ensemble
du plan est un ensemble  de disques ouverts dont la réunion contient
de disques ouverts dont la réunion contient  (dans l'espace, on remplace les disques par des boules).
(dans l'espace, on remplace les disques par des boules).
2) Un recouvrement  de
de  est dit plus fin que
est dit plus fin que  si
si  .
.
3) L'ordre d'un recouvrement  de
de  est l'entier
est l'entier  .
.
Définition de la dimension topologique d'un compact par recouvrements:
1) Soit  . On dit que
. On dit que  si tout recouvrement fini de
si tout recouvrement fini de  possède un recouvrement plus fin d'ordre
possède un recouvrement plus fin d'ordre  .
.
2) On dit que  si on a
si on a  , mais pas
, mais pas  .
.
On peut aisément se convaincre par un dessin que la dimension topologique par recouvrements de l'ensemble de Cantor est nulle, tandis que celle du tamis de Sierpinski est 1.
Malheureusement, cette définition de la dimension par un entier ne semble pas refléter toutes les propriétés observables : par exemple, un cercle et le flocon de Koch sont tous deux de dimension topologique 1, alors que le premier a une longueur finie, et le second pas.
Cette remarque justifie l'introduction de nouveaux types de dimensions, pouvant prendre des valeurs non entières.
De cette façon, on s'attend à ce que le flocon de Koch ait une dimension inférieure à celle du tamis de Sierpinski, car il "remplit moins" le plan, mais supérieure à celle du cercle, dont la dimension doit rester égale à 1.
Autrement dit, les fractals auront droit à une dimension "fractionnaire", qui devra rendre compte de leur position vis-à-vis des repères habituels que sont le point, la ligne, la surface et le volume intuitifs.
B ] Notions d'auto-similitude
Pour introduire la notion de dimension fractionnaire, il est nécessaire d'abord de définir quelques propriétés géométriques souvent liées aux fractals.
Rappelons d'abord qu'une similitude (directe) est une transformation qui peut s'écrire comme la composée d'un déplacement et d'une homothétie. Elle multiplie toutes les longueurs par un rapport constant, et conserve (dans le plan) les angles orientés de vecteurs. Deux figures qui se déduisent l'une de l'autre par une similitude sont dites semblables.
On dit alors qu'un compact  est (strictement) auto-semblable en un point
est (strictement) auto-semblable en un point  si dans tout disque (ou boule) de centre
si dans tout disque (ou boule) de centre  , il existe un sous-ensemble de
, il existe un sous-ensemble de  qui est semblable à
qui est semblable à  .
.
Un exemple : imaginons un livre dont la couverture est formée par un dessin d'une main tenant le livre lui-même.
Sur le livre dessiné est également redessiné le livre, et ceci jusqu'à l'infini, même si on ne le voit pas. De plus, les livres successifs vont se rapetisser jusqu'à tendre vers un point. Alors la couverture initiale du livre est strictement auto-semblable en ce point-limite.
De même, la fougère de Barnsley est auto-semblable en toute feuille, mais pas en un point appartenant à une tige, par exemple (ici aussi, une feuille est en fait un point-limite).
Par extension, on dit qu'un compact est (strictement) auto-semblable s'il l'est en tout point.
Par exemple, la courbe de Koch est auto-semblable. Pour s'en convaincre, il suffit d'exécuter Courbe_de_Koch à un rang suffisant pour que la différence avec le rang précédent ne soit plus perceptible, et d'effectuer un zoom sur l'image. On a l'impression que l'image n'a pas changé, alors qu'en réalité on ne voit plus qu'une partie de l'image !
De même, le tamis de Sierpinski et l'ensemble de Cantor sont auto-semblables.
Ces deux notions d'auto-similitude peuvent se généraliser :
1) D'abord, il peut arriver qu'au lieu d'y avoir aussi près d'un point que l'on veut une copie semblable au tout, il n'y ait que des copies déformées, c'est-à-dire se déduisant du tout par une application affine quelconque : on parle alors d'auto-affinité.
2) Ensuite, et c'est le cas dans la nature, mais aussi dans des fractals très déterministes, il se peut que l'auto-similitude ne soit qu'approximative, ou vraie seulement si l'on considère qu'on ne s'approche pas du point de façon infinitésimale : c'est le cas du chou-fleur, mais aussi du fractal obtenu en appliquant l'IFS feu.
On parle alors d'auto-similitude ou d'auto-affinité statistiques.
Attention !
1) On l'a vu dans certains exemples, ces propriétés, même lorsqu'elles sont vérifiées par l'attracteur d'un IFS, ne sont en général pas vérifiées par les approximations successives de l'attracteur obtenues en appliquant un nombre fini de fois cet IFS.
Ceci impose bien évidemment un obstacle infranchissable à l'étude de ces notions sur un écran d'ordinateur, puisqu'on ne peut tracer l'attracteur, mais que des approximations. Même mathématiquement parlant, ces approximations, aussi précises soient elles, ne permettent pas un raisonnement sur l'attracteur.
On est donc dans la majorité des cas limité à l'observation d'une auto-similitude statistique, et en tout cas la notion d'auto-similitude est difficile à quantifier.
2) Un compact n'a pas besoin d'être un fractal pour être auto-semblable : penser au cas d'un segment.
C ] Dimension d'homothétie
L'idée est fondée sur la propriété d'auto-similitude stricte.
Prenons un premier exemple :
Supposons qu'on veuille remplir ce cube avec des modèles réduits de ce cube, l'échelle étant . Il faudra alors utiliser
. Il faudra alors utiliser  petits cubes. Si l'on fait pareil pour un carré, la relation est
petits cubes. Si l'on fait pareil pour un carré, la relation est  , et pour un segment on obtient
, et pour un segment on obtient  .On remarque que l'exposant
.On remarque que l'exposant  dans ce type de relation se trouve coïncider avec la dimension universellement admise de ces objets qui, s'ils ne sont pas de nature fractale, n'en sont pas moins auto-semblables.
dans ce type de relation se trouve coïncider avec la dimension universellement admise de ces objets qui, s'ils ne sont pas de nature fractale, n'en sont pas moins auto-semblables.
Cet exemple était évidemment simpliste. Que se passe-t'il si on considère la courbe de Koch, qui est également auto-semblable ?
Dans ce cas, on va pour des raisons évidentes se limiter à des échelles du type  . On a alors
. On a alors  , ce qui nous donne
, ce qui nous donne  . Par analogie avec l'exemple précédent, on posera que la dimension d'homothétie de la courbe de Koch est
. Par analogie avec l'exemple précédent, on posera que la dimension d'homothétie de la courbe de Koch est  .
.
En appliquant cette méthode, on trouve que la dimension d'homothétie de l'ensemble de Cantor vaut  , et que celle du tamis de Sierpinski vaut
, et que celle du tamis de Sierpinski vaut  .
.
Ces mesures reflètent bien ce qu'on observe, à savoir que l'ensemble de Cantor est quelque chose d'intermédiaire entre un ensemble de points isolés et une ligne, tandis que le tamis de Sierpinski est plus proche de la surface que de la ligne, contrairement à la courbe de Koch.
D ] Dimension par compas (ou par divisions successives)
Cette définition de la dimension s'applique à des courbes. Elle s'appuie sur une observation des courbes fractales auto-semblables, comme un segment ou la courbe de Koch.
Supposons qu'au lieu de compter le nombre de modèles réduits à l'échelle  de la courbe de Koch nécessaires pour reconstituer toute la courbe, l'on prenne un écartement de compas de
de la courbe de Koch nécessaires pour reconstituer toute la courbe, l'on prenne un écartement de compas de  , que l'on reporte sur la courbe à partir d'une extrémité jusqu'à l'autre, et que l'on mesure la longueur de la ligne brisée ainsi tracée. Par le choix particulier de cet écartement de compas, il se trouve que cette ligne brisée coïncide exactement avec courbe_de_Koch(p), et a donc pour longueur
, que l'on reporte sur la courbe à partir d'une extrémité jusqu'à l'autre, et que l'on mesure la longueur de la ligne brisée ainsi tracée. Par le choix particulier de cet écartement de compas, il se trouve que cette ligne brisée coïncide exactement avec courbe_de_Koch(p), et a donc pour longueur  . Donc
. Donc  . On remarque donc que
. On remarque donc que  . Si l'on fait de même avec un segment de longueur 1, et un écartement de
. Si l'on fait de même avec un segment de longueur 1, et un écartement de  , on aboutit à
, on aboutit à  , et on retrouve encore la dimension d'homothétie du segment.
, et on retrouve encore la dimension d'homothétie du segment.
A la suite de cette observation, on peut remarquer que l'auto-similitude du segment et de la courbe de Koch n'ont servi qu'à aider à un choix judicieux des écartements de compas permettant un calcul exact de la longueur de la ligne brisée. Il se trouve que si on avait choisi des écartements arbitraires  tendant vers zéro, la formule
tendant vers zéro, la formule  n'aurait été rigoureusement exacte que pour les valeurs particulières choisies plus haut. Néanmoins, pour d'autres valeurs, l'erreur tend vers zéro, car elle ne provient que des "coins sautés" lors de la construction d'une ligne brisée ne coïncidant plus exactement avec une approximation par IFS de la courbe de Koch.
n'aurait été rigoureusement exacte que pour les valeurs particulières choisies plus haut. Néanmoins, pour d'autres valeurs, l'erreur tend vers zéro, car elle ne provient que des "coins sautés" lors de la construction d'une ligne brisée ne coïncidant plus exactement avec une approximation par IFS de la courbe de Koch.
On obtient donc  .
.
Ceci permet d'en déduire une généralisation de la dimension d'homothétie à des courbes qui ne sont plus que statistiquement auto-semblables. En voici le principe :
Choisissons une longueur  donnée (l'écartement du compas), partons d'une extrémité de la courbe jusqu'à l'autre en reportant le compas de telle manière que tous les points ainsi tracés soient sur la courbe. On obtient ainsi une ligne brisée dont tous les sommets sont sur la courbe. Soit
donnée (l'écartement du compas), partons d'une extrémité de la courbe jusqu'à l'autre en reportant le compas de telle manière que tous les points ainsi tracés soient sur la courbe. On obtient ainsi une ligne brisée dont tous les sommets sont sur la courbe. Soit  la longueur de cette ligne brisée.
la longueur de cette ligne brisée.
S'il existe  tels que
tels que  , alors le nombre
, alors le nombre  est appelée la dimension par compas de la courbe.
est appelée la dimension par compas de la courbe.
(le nombre  valait 1 dans la présentation ci-dessus parce qu'on avait supposé les extrémités de la courbe distantes de 1 unité)
valait 1 dans la présentation ci-dessus parce qu'on avait supposé les extrémités de la courbe distantes de 1 unité)
On doit donc avoir  , ce qui fait que dans la pratique, et particulièrement avec des courbes présentant une auto-similitude statistique, on construit l'ensemble des points
, ce qui fait que dans la pratique, et particulièrement avec des courbes présentant une auto-similitude statistique, on construit l'ensemble des points 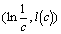 , que l'on cherche ensuite à approximer par une droite en utilisant la méthode de régression linéaire. Si la dimension par compas de la courbe existe, la pente de cette droite doit être pratiquement constante lorsqu'on augmente le nombre de mesures en diminuant l'écartement du compas. Cette constante est alors la dimension cherchée.
, que l'on cherche ensuite à approximer par une droite en utilisant la méthode de régression linéaire. Si la dimension par compas de la courbe existe, la pente de cette droite doit être pratiquement constante lorsqu'on augmente le nombre de mesures en diminuant l'écartement du compas. Cette constante est alors la dimension cherchée.
Par exemple, si l'on tente cette expérience sur la côte de la Grande-Bretagne, en prenant des cartes de plus en plus détaillées, on est frappé de voir que les points du diagramme log-log sont très bien alignés, sur une droite de pente  . On en déduit que cette côte est une courbe fractale de dimension par compas à peu près égale à
. On en déduit que cette côte est une courbe fractale de dimension par compas à peu près égale à  .
.
La côte britannique est donc plus intriquée que la côte de l'île de Koch !
Conformément à ce qu'on pense, si on réalise cette expérience sur un segment, un cercle ou toute autre courbe "normale",  tend évidemment vers la longueur
tend évidemment vers la longueur 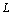 de la courbe, ce qui donne
de la courbe, ce qui donne  , et donc la dimension par compas d'une telle courbe vaut bien 1.
, et donc la dimension par compas d'une telle courbe vaut bien 1.
D'ailleurs, par construction, les dimensions par compas et par homothétie de courbes auto-semblables sont les mêmes.
Résumons : nous avons défini deux types de dimensions fractionnaires.
1) La dimension d'homothétie, qui s'applique aux fractals de toute nature, à condition qu'ils soient auto-semblables.
2) La dimension par compas, qui s'applique à tout type de courbe fractale.
Ces deux définitions coïncident sur l'intersection de leurs champs d'application.
Mais il faut savoir que le débat scientifique sur la dimension n'est pas clos, et qu'il existe ainsi une bonne dizaine de définitions, qui parfois s'appliquent à des objets de nature distinctes, et qui, lorsqu'elles s'appliquent à des objets communs, donnent parfois les mêmes valeurs, et parfois pas ! Néanmoins, prises chacune à part, elle permettent souvent de comparer des objets de même nature.
Nous allons encore définir une troisième notion de dimension fractale, dont l'intérêt est qu'elle est facile à mettre en pratique sur le plan informatique.
E ] La dimension par recouvrement
Le principe de cette définition est encore lié à l'origine à la notion d'auto-similitude statistique.
Pour fixer les idées, supposons que l'on prenne un objet fractal dans le plan, et que l'on dispose d'une infinité de grilles rectangulaires de même taille, à mailles carrées, ayant les propriétés suivantes :
1) La taille commune suffit à recouvrir tout le fractal.
2) Le maillage des grilles est formé de carrés isométriques de plus en plus petits.
(on voit immédiatement que ce format de grille peut être réalisé à l'aide d'un écran d'ordinateur, la taille des mailles étant lié à un choix de résolution)
Remarque : si on travaillait dans l'espace, on prendrait un maillage en trois dimensions.
Pour un maillage donné, on compte le nombre de mailles qui contiennent au moins un point appartenant au fractal, et on étudie la relation entre la finesse du maillage et le nombre de mailles atteintes. Plus précisément, dans la pratique, on prend un lot de grilles dont le maillage se déduit du maillage initial par une subdivision de chaque maille en  mailles identiques, et on compte le nombre
mailles identiques, et on compte le nombre  mailles atteintes par le fractal. Puis on calcule le nombre
mailles atteintes par le fractal. Puis on calcule le nombre  (c'est le taux d'accroissement logarithmique du nombre de cases en fonction de la finesse), et on définit la limite de cette expression lorsque
(c'est le taux d'accroissement logarithmique du nombre de cases en fonction de la finesse), et on définit la limite de cette expression lorsque  comme la dimension par recouvrement du fractal.
comme la dimension par recouvrement du fractal.
On peut vérifier que cette nouvelle dimension fractale coïncide avec les deux autres pour des formes géométriques simples, mais aussi pour la courbe de Koch et la côte de la Grande-Bretagne, par exemple. C'est cependant la dimension par recouvrement qui est la plus utilisée, car son estimation est susceptible d'une programmation informatique. D'autre part, elle présente une certaine cohérence car elle donne toujours une valeur entre 1 et 2 dans le plan, ce qui n'est pas le cas par exemple de la dimension d'homothétie, puisqu'on peut construire des courbes fractales auto-semblables de dimension d'homothétie strictement supérieure à 2, en prenant par exemple des courbes ayant des points multiples.