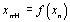, avec 
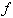fonction polynôme du second degré.
CHAPITRE 1:L'ITERATEUR QUADRATIQUE
FICHIER MAPLE CORRESPONDANT : ITE-QUAD.MWS
A ] Introduction
Il s'agit d'un système dynamique discret du type 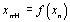, avec 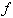fonction polynôme du second degré.
Dans la pratique, on prend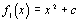 
, ou 
ou 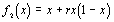encore 
.
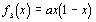On peut montrer que les trois systèmes dynamiques correspondant ont un comportement qualitatif équivalent (voir Appendice). Le premier a une interprétation intéressante dans le champ complexe (voir chapitre 6), tandis que le second a un intérêt historique majeur, puisque c'est lui qui a permis de mettre en évidence pour la première fois un comportement chaotique dans un processus naturel.
En effet, le mathématicien belge Pierre François Verhulst a étudié en 1845 l'évolution de certaines populations animales en fonction du temps. En notant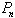 
le nombre d'individus à l'instant 
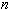(mesuré en minutes, heures, jours, ou années...), il s'agissait de trouver un modèle mathématique donnant 
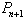en fonction de 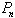. Il existe en fait un grand nombre de paramètres qui interviennent: nourriture, espace vital, climat, etc..., mais le propre d'un modèle est de supposer constants le plus grand nombre possible de paramètres. Le modèle de Verhulst suppose que le taux de croissance 
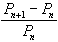est proportionnel à 
, où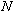 
désigne le maximum que la population ne peut pas dépasser, et dont l'existence est évidente. Si on appelle 
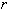la constante de proportionnalité, et 
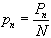, on aboutit au modèle logistique 
, avec de surcroît 
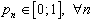. Il s'est avéré que ce modèle correspond bien aux observations réelles.
Pour les besoins de la cause, nous allons observer ce qui se passe avec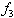 
, où 
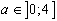, et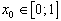 
.
B ] Observations
Le programme MAPLE itérateur propose une implémentation de l'itérateur quadratique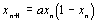 
, dont la progression des 20 premiers termes est graphiquement visualisée sous la forme classique.
Il y a ensuite divers choix du paramètre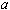 
(1, 1.75, 2, 2.75, 3.1, 3.5, 3.6, 3.83, et 4), avec différentes valeurs initiales 
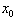. On ne dépasse pas 4 car sinon la suite pourrait s'échapper de 
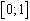. Vous pouvez évidemment tester d'autres valeurs initiales.
Les abscisses des points d'intersection du graphe de 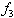avec la première bissectrice sont les points fixes de l'itérateur, et on démontre que ce sont les seules limites possibles de la suite 
.
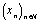Pour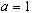 
, on constate que la suite converge vers 
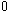, indépendamment de la valeur initiale 
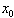: on dit que 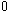est un point fixe attractif.
Pour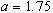 
, il y a un autre point fixe, qui est attractif, tandis que 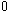reste un point fixe, mais toute valeur initiale 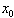différente 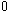de et de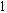 
envoie inéluctablement la suite vers le point attractif: on dit que 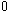est un point fixe répulsif.
Pour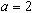 
, on observe un phénomène analogue, mais le point fixe attractif 
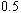est super-attractif (convergence très rapide).
Jusqu'à présent, la convergence vers le point fixe attractif s'est faite en escalier. Ceci est vrai pour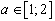 
.
Pour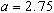 
, ce qui change est le mode de convergence vers le point fixe attractif: il y a convergence en spirale.
Ceci s'observe pour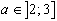 
, la convergence pour les valeurs proches de 
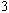pouvant être très lente.
Au-delà de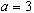 
, le point fixe non nul devient à son tour répulsif, et il apparaît un cycle attractif de période 2, les points de la suite semblant se rapprocher alternativement de plus en plus de chacun des deux points du cycle. Ceci peut s'observer pour 
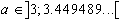, par exemple pour 
.
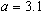Entre 
, le cycle de période 2 devient à son tour répulsif, et il apparaît un cycle attractif de période 4 (voir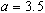 
). Ensuite (entre 
), il apparaît un cycle attractif de période 8,etc...
En passant ainsi des seuils successifs correspondant à des valeurs croissantes de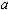 
, on fait apparaître un nouveau cycle attractif de période double, tandis que les cycles précédents deviennent répulsifs, c'est à dire qu'on ne peut plus les atteindre qu'en choisissant pour 
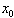l'une des valeurs du cycle.
Cette suite de seuils tend vers une limite, appelée Point de Feigenbaum, et qui vaut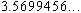 
En deçà de cette limite, l'attracteur de l'itérateur quadratique - c'est-à-dire l'ensemble des points que les éléments de la suite approchent d'aussi près que l'on veut - est, on l'a vu, formé de l'ensemble fini des points d'un cycle de période 
. Au-delà, les valeurs prises par les éléments de la suite semblent se distribuer de façon imprévisible, mais homogène dans un certain sous-ensemble de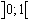 
, dépendant de 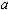(essayer 
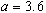, en augmentant éventuellement le nombre (fixé à 20) des valeurs calculées dans la suite dans la procédure itérateur).
Ceci marque l'entrée dans ce qu'on appelle un comportement chaotique: l'attracteur est dense dans une réunion de sous-intervalles de 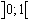. On appelle ce type d'attracteur un attracteur étrange (voir chapitre 5).
La notion de chaos sera précisée au chapitre 2.
Pour ajouter un peu de mystère à ce qui se passe après le Point de Feigenbaum, on peut remarquer certaines plages de valeurs de 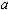, situées entre le Point de Feigenbaum et 4, et dans lesquelles le comportement de l'itérateur quadratique cesse brusquement d'être chaotique, l'attracteur prenant momentanément de nouveau la forme d'un cycle périodique (voir 
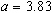). Pour une étude plus complète de l'itérateur quadratique, une introduction à la Constante universelle de Feigenbaum, ainsi qu'une illustration du théorème de Charkovsky, se reporter au chapitre 4.
1) 
, en posant 
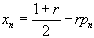et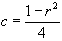 
.
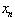étant fonction affine de 
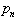, les comportements de ces deux suites sont équivalents, qu'elles soient convergentes, périodiques ou chaotiques.
2) 
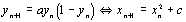, en posant 
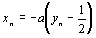et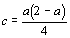 
.
Et on retrouve là aussi une relation affine entre 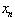et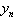 
.