CHAPITRE 4 :LA CONSTANTE UNIVERSELLE DE FEIGENBAUM

FICHIER MAPLE CORRESPONDANT : FEIGENBAUM.MWS

A ] Les bifurcations de Feigenbaum

Comme on l'a vu dans le chapitre 1, l'itérateur quadratique possède un attracteur qui dépend de . Pour tenter de visualiser les variations de cet attracteur en fonction du paramètre , on peut utiliser la procédure feigenbaum, qui admet trois arguments :

- début et fin sont les bornes respectivement inférieure et supérieure de l'intervalle des paramètres que l'on veut visualiser.

- pas est la distance que l'on prend entre deux points consécutifs de l'intervalle considéré.

Plus l'intervalle est étroit, plus on a intérêt à choisir pas petit, mais il faut naturellement tenir compte de la vitesse et surtout de la mémoire de la machine. On pourra aussi modifier le test d'arrêt de compteurs de boucle k au sein de la procédure.

Dans un premier temps, feigenbaum(1,4,pas) , où pas est à définir (par exemple 0.01), permet de visualiser les variations générales. On obtient ce qu'on appelle le diagramme de Feigenbaum.

Comme on l'a vu dans le chapitre 1, l'attracteur est d'abord formé d'un unique point, qui est le point fixe attractif de l'itérateur. Puis apparaissent successivement les cycles de longueur 2, 4, 8, ..., pour des valeurs successives des paramètres qu'une utilisation patiente et minutieuse de la procédure feigenbaum permet de déterminer aussi précisément que l'on veut. Ces nombres s'appellent les paramètres de bifurcation de l'itérateur quadratique.

On peut vérifier que les premiers termes de cette suite sont :

Pour s'en convaincre, on pourra exécuter feigenbaum avec les arguments proposés. Les graphiques obtenus semblent situer les points un peu à gauche des valeurs réelles. Ceci vient du fait que ces valeurs représentent des points de passage à la répulsivité des points précédemment attractifs. Juste avant la bifurcation, l'attraction de ces points attractifs devenant très faible, il faut attendre plus longtemps pour assister à la convergence. Il en résulte que si l'on voulait mieux montrer que le passage se produit à cet endroit, il faudrait laisser tomber plus de termes initiaux (50 dans feigenbaum). Essayez en prenant provisoirement 200 dans feigenbaum(2.9,3.1,0.005) pour voir la différence...

B ] Vers le point de Feigenbaum

Il est clair en exécutant feigenbaum que la progression des bifurcations tend vers une certaine limite. Cette limite s'appelle le Point de Feigenbaum, et possède donc la propriété suivante qui rend compte de ce qui se passe à sa gauche:

pour tout , il existe tel que tous les paramètres correspondent à des cycles de longueur , avec .

Reprenons la suite des bifurcations :

Cette suite converge vers . Comment parvient-on à cette approximation ?

On peut évidemment envisager de faire tourner un programme de type feigenbaum sur un ordinateur puissant pour calculer de façon très précise un grand nombre de bifurcations successives, et obtenir ainsi avec une précision du même ordre le point de Feigenbaum. Mais cette méthode a le désavantage d'être trop dépendante dans sa fiabilité du choix du terme initial dont on observe l'orbite pour construire l'attracteur correspondant à un paramètre donné (on a pu mesurer cette dépendance dans la petite expérience du paragraphe précédent).

Il existe une méthode plus fiable, qui consiste à observer que, si désigne l'itérateur , on a :

1) Pour , possède exactement 1 point fixe, qui varie grosso modo entre 0 et 0,75 , et qui vaut 0,5 pour .

2) Pour , possède exactement 2 point fixes (les points qui forment l'attracteur de ), le premier variant entre 0,44 et 0,65, l'autre entre 0,65 et 0,84. Il existe donc une unique valeur pour laquelle 0,5 est point fixe de .

3) Pour , possède exactement 4 points fixes (les points qui forment l'attracteur de ), variant dans quatre intervalles disjoints dont un seul contient 0,5, cette valeur étant un point fixe de pour une unique valeur du paramètre .

On construit ainsi une suite , de paramètres vérifiant les propriétés suivantes :

a) .         b) .

La première propriété implique que la suite converge vers le point de Feigenbaum. Et c'est la deuxième qui va nous permettre une détermination explicite des termes de cette suite, en même temps qu'une preuve de son existence. En effet, si l'on prend par exemple , ce nombre est la solution dans l'intervalle de l'équation en : , et si l'on prend , ce nombre est la solution autre que dans l'intervalle de l'équation en : , qui s'écrit plus simplement . On sait que 2 est solution , et on peut donc trouver les racines qui sont , ce qui donne finalement .

Malheureusement, la détermination de impose la résolution d'une équation algébrique de degré dont on ne connaît que les solutions . On est donc amené à utiliser une méthode d'approximation numérique. Il se trouve que la méthode de Newton s'applique très bien à ce problème.

Remarque :

Du point de vue analytique, pour le paramètre , le point fixe 0.5 est super-attractif pour , puisque la dérivée de cette fonction s'annule au point fixe (on avait déjà observé ce phénomène pour dans le chapitre 1). En effet, , et par suite .

C ] La Constante universelle de Feigenbaum

La découverte de cette constante est due entièrement au mathématicien Mitchell J. Feigenbaum, qui l'a calculée à l'aide d'une simple calculette vers 1975. Il avait observé que les bifurcations de l'itérateur quadratique convergeaient vers leur limite d'une façon "régulière". Ceci peut se voir en modifiant légèrement la procédure feigenbaum en ressemblance_dans_feigenbaum, dans laquelle on impose un intervalle pour les ordonnées, réalisant ipso facto la possibilité de faire un zoom sur une partie du graphique général. Les deux exemples proposés montrent qu'en choisissant bien la partie du graphique sur laquelle on applique le zoom, on retrouve un graphique (statistiquement) semblable.

Il a donc été conduit à étudier la suite et il a remarqué qu'elle se conduisait presque comme une suite géométrique. Presque, car le rapport n'est pas constant, mais tend vers une limite .

Avec les valeurs de que l'on a, cela donne

Feigenbaum est ainsi arrivé à

Ce nombre est la Constante de Feigenbaum. On le retrouve dans un grand nombre de phénomènes liés aux systèmes dynamiques, dans des domaines aussi variés que l'hydrodynamique, l'électronique, l'acoustique et le laser. Nous le retrouverons d'ailleurs dans les chapitres suivants. Il a donc un caractère "universel", au même titre par exemple que le nombre .

Remarque :

Pour calculer des approximations de la constante de Feigenbaum, on peut utiliser la suite , dont la limite est également .

D ] Au point de Feigenbaum

Le point de Feigenbaum n'étant pas connu de façon exacte, il est impossible de visualiser ce qui se passe en ce point. Néanmoins, on peut l'imaginer assez simplement. Supposons la suite constante égale à , et les différentes branches qui se développent à chaque bifurcation schématisées par des segments.
On peut remarquer que pour effectuer les zooms du paragraphe C], on a appliqué verticalement un rapport approximatif de 2.3 , et horizontalement un rapport de .

On peut donc schématiser le graphique obtenu par feigenbaum(1,4,pas) par celui obtenu à l'aide du programme récursif MAPLE arbre_de_Feigenbaum (on remarquera que l'on construit ainsi un superbe fractal strictement auto-affine en ses feuilles).

Ceci schématise ce qu'on appelle l'arbre des périodes doublantes dans le diagramme de Feigenbaum, c'est à dire la partie du diagramme correspondant à .

Sur ce graphique, l'arbre pousse de telle façon qu'à la limite les feuilles représentent une schématisation de l'attracteur au point de Feigenbaum. Et on se convainc ainsi aisément que cet attracteur est un ensemble du type ensemble de Cantor (bien qu'il soit ici dense dans ). On a donc un attracteur qui n'est plus fini, comme pour les paramètres précédents, mais qui ne contient cependant aucun intervalle, alors que lorsque le comportement est chaotique l'attracteur est souvent une réunion d'intervalles. Une fois de plus, on constate que le point de Feigenbaum est un seuil de passage...

E ] Après le point de Feigenbaum

Nous allons maintenant étudier ce qui se passe pour .

Pour , l'étude a été faite de façon très approfondie au chapitre 2, et a même servi de modèle de comportement chaotique dans un système dynamique. On a vu en particulier que l'attracteur était égal au segment , avec cependant une distribution non uniforme des points de l'orbite d'un point ergodique dans l'attracteur (revoir histogramme dans CHAOS.MWS).

En exécutant feigenbaum(3.55,4,0.005), on fait immédiatement quatre constatations :

1) L'attracteur semble ne devenir un intervalle qu'à partir d'une certaine valeur .

2) Pour , cet intervalle s'élargit progressivement jusqu'à .

3) Pour , l'attracteur est une réunion finie d'intervalles, et l'on peut percevoir l'existence d'une suite strictement décroissante de valeurs de : convergeant vers , qui représentent des points où l'attracteur voit doubler le nombre des intervalles qui le composent.

4) Il semble y avoir des "plages" de paramètres plus ou moins larges, un peu partout entre et 4, pour lesquelles le comportement n'est pas chaotique, mais où au contraire l'attracteur semble se réduire à un cycle fini.

5) Les zones remplies par les points du graphique semblent circonscrites par des courbes, qui résultent en fait de l'accumulation d'un grand nombre de points au voisinage de ces "courbes".

Les trois premières constatations ont une allure de déjà-vu. Le scénario consistant à doubler quelque chose en des points donnés a été rencontré lors de l'étude de la suite des bifurcations de Feigenbaum. La suite joue donc un rôle analogue à la suite , ces deux suites ayant la même limite, les termes de même rang correspondant au passage à un attracteur comportant respectivement points et intervalles.

C'est à cause de cette analogie que la partie du diagramme de Feigenbaum correspondant à s'appelle le reflet chaotique de l'arbre des périodes doublantes.

Remarque :

On montre que, de façon remarquable, la suite vérifie comme son homologue la propriété , et on retrouve ainsi la constante de Feigenbaum !

Les bandes à attracteur périodique sont, elles, plus surprenantes : tentons pour y voir plus clair d'obtenir des agrandissements successifs de la plus importante d'entre elles, celle correspondant à .

Réalisons à cet effet les appels de feigenbaum proposés dans FEIGENBAUM.MWS.

Le premier agrandissement laisse clairement apparaître un intervalle de paramètres où l'attracteur est un cycle de période 3, ce que confirme le second agrandissement (les valeurs sporadiques de où des points apparaissent ailleurs sont des valeurs pour lesquelles la convergence vers l'attracteur est très lente, ce qui fait que même après le cinquantième itéré, l'orbite n'est pas encore stabilisée).

Mais le premier agrandissement laisse également entrevoir comment on entre dans cette bande, et comment on en sort.

On y entre de façon brutale : d'un coup, l'orbite cesse d'être chaotique, et devient cyclique. Pour la bande étudiée, cela se passe pour , et cela correspond à la valeur pour laquelle possède un point fixe super-attractif. Toutes les autres bandes ont le même comportement à l'entrée, qui s'interprète par la super-attractivité d'un point fixe d'un itéré de . Le rang de cet itéré est alors égal à la période du cycle caractérisant la bande en question.

Pour la sortie, elle semble reproduire ce qui se passait juste avant le point de Feigenbaum : un doublement successif de la période. La différence est que la suite des périodes des cycles ainsi obtenue, au lieu d'être la suite des puissances de 2, est le produit de cette suite par la période initiale (dans notre cas, la suite ).

Une question se pose alors : combien y a-t-il de telles bandes à attracteurs cycliques, et quelles en sont les périodes ?

En fait il existe une infinité de bandes de ce type :

1) Dans se trouvent des bandes principales de période c'est-à-dire les impairs supérieurs à 1, et ce de la droite vers la gauche. On distingue les premières sur le graphique feigenbaum(3.55,4,0.005, mais les suivantes sont trop étroites pour être visibles.

2) Dans , on trouve, toujours en allant vers la gauche, des bandes de période , c'est-à-dire les doubles des impairs.

3) Plus généralement, dans , on trouve comme bandes principales les bandes de période

Cette suite de périodes est appelée la suite de Charkovsky.

En effet, supposons l'ensemble des entiers naturels non nuls ordonné par la relation :

Le théorème de Charkovsky affirme que si une application admet un point de période (c'est-à-dire ), alors admet des points de toute période telle que .

Ceci permet de prévoir par exemple que pour tout paramètre appartenant à la bande de période 3, l'itérateur quadratique correspondant admet des points de toute période, puisque 3 est le plus petit élément pour cet ordre. On ne les voit pas sur notre graphique, car ce sont des cycles répulsifs.

Remarquons que la dernière partie de la suite de Charkovsky, celle correspondant aux périodes puissances de 2, est atteinte au fur et à mesure de la descente de l'arbre aux périodes doublantes.

En fait, on démontre théoriquement quelque chose de plus que l'existence de cycles attractifs de toute période dans le diagramme de Feigenbaum : il existe dans tout sous-intervalle de une bande correspondant à un attracteur cyclique. On peut appeler cela la densité des attracteurs cycliques dans le diagramme de Feigenbaum.

Il nous reste à étudier le problème de ces courbes d'accumulation dans cette deuxième partie du diagramme de Feigenbaum. étant donné l'algorithme de construction du diagramme, ces courbes sont visibles parce qu'il y a, pour un paramètre donné, un grand nombre d'itérés du point initial 0.1 qui s'accumulent en certains points. Nous avions déjà pu vérifier ce phénomène pour , à l'aide de la procédure histogramme dans CHAOS.MWS : il y avait un grand nombre d'itérés proches de 0 et de 1.

En fait, ces valeurs d'accumulation sont les valeurs prises par Elles sont généralement en nombre infini, mais la plupart d'entre elles n'apparaissent pas sur les graphiques à cause du relativement petit nombre d'itérés calculés pour construire ces graphiques.

Les courbes 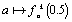sont appelées les lignes critiques du reflet chaotique dans le diagramme de Feigenbaum. Pour visualiser les premières, exécuter display({lignes_critiques(k)}), puis, pour voir le rapport qu'elles ont avec le diagramme de Feigenbaum, on pourra exécuter display({lignes_critiques(k),feigenbaum(3.55,4,0.01)}).

Chapitre précédent Sommaire Chapitre suivant