 , où
, où  désigne un paramètre complexe. On peut faire une première remarque simple sur les orbites
désigne un paramètre complexe. On peut faire une première remarque simple sur les orbites 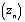 par itération de
par itération de  : si
: si  , alors
, alors  . En effet, posons
. En effet, posons  . On a alors
. On a alors  . En continuant de proche en proche, on en déduit que pour
. En continuant de proche en proche, on en déduit que pour  , on a
, on a  .
.
CHAPITRE 6 :LES ENSEMBLES DE JULIA ET L'ENSEMBLE DE MANDELBROT
FICHIER MAPLE CORRESPONDANT : JULIA-MANDELBROT.MWS
A ] Définition des ensembles de Julia
Nous allons considérer dans ce chapitre la famille des applications du plan dont l'expression complexe est  , où
, où  désigne un paramètre complexe. On peut faire une première remarque simple sur les orbites
désigne un paramètre complexe. On peut faire une première remarque simple sur les orbites 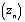 par itération de
par itération de  : si
: si  , alors
, alors  . En effet, posons
. En effet, posons  . On a alors
. On a alors  . En continuant de proche en proche, on en déduit que pour
. En continuant de proche en proche, on en déduit que pour  , on a
, on a  .
.
On peut donc considérer que le bassin d'attraction du "point à l'infini" du plan complexe contient l'extérieur d'un disque dont le rayon ne dépend que de  . Ce bassin d'attraction, constitué de l'ensemble des points initiaux dont l'orbite s'échappe vers l'infini, est appelé l'ensemble des fugitifs pour
. Ce bassin d'attraction, constitué de l'ensemble des points initiaux dont l'orbite s'échappe vers l'infini, est appelé l'ensemble des fugitifs pour  , tandis que son complémentaire, formé de l'ensemble des points dont l'orbite est bornée, est appelé l'ensemble des prisonniers
, tandis que son complémentaire, formé de l'ensemble des points dont l'orbite est bornée, est appelé l'ensemble des prisonniers .
.
On définit alors l'ensemble de Julia  pour
pour  comme la frontière entre l'ensemble des fugitifs et celui des prisonniers, autrement dit l'ensemble des points dont tout voisinage contient au moins un point de chacun des deux types.
comme la frontière entre l'ensemble des fugitifs et celui des prisonniers, autrement dit l'ensemble des points dont tout voisinage contient au moins un point de chacun des deux types.
Examinons d'abord un cas très particulier, celui de  . Dans ce cas, il est clair que
. Dans ce cas, il est clair que  , et que donc l'orbite de
, et que donc l'orbite de  est bornée si et seulement si
est bornée si et seulement si  . On en déduit que
. On en déduit que  est le disque fermé de centre l'origine et de rayon 1, tandis que
est le disque fermé de centre l'origine et de rayon 1, tandis que  est le cercle correspondant. De plus, tous les points intérieurs au disque ont une orbite qui converge vers l'origine, tandis que ceux du cercle ont une orbite qui reste sur le cercle.
est le cercle correspondant. De plus, tous les points intérieurs au disque ont une orbite qui converge vers l'origine, tandis que ceux du cercle ont une orbite qui reste sur le cercle.
Cette dernière propriété se retrouve dans tous les ensembles de Julia, mais c'est bien la seule ! En effet, les ensembles de Julia sont en général des objets fractals aussi compliqués que divers, et la dynamique à l'intérieur de l'ensemble des prisonniers (quand cet intérieur est non vide !) est souvent surprenante. La seule régularité qu'ils possèdent est la symétrie par rapport à l'origine, du fait de la parité de  , symétrie que nous exploiterons lors de leur construction.
, symétrie que nous exploiterons lors de leur construction.
La procédure julia1 permet de visualiser grossièrement quelques ensembles de prisonniers. On voit que l'on trouve aussi bien des morceaux "d'un bloc", dont l'ensemble de Julia est visiblement une courbe fractale, que des ensembles de prisonniers qui semblent eux-mêmes être une courbe (ce sont des dendrites, voir  ), ou encore des ensembles de prisonniers qui semblent s'effilocher de plus en plus au fur et à mesure que l'on augmente la profondeur de recherche. L'algorithme pour construire ces ensembles reprend leur définition : on quadrille le disque de rayon
), ou encore des ensembles de prisonniers qui semblent s'effilocher de plus en plus au fur et à mesure que l'on augmente la profondeur de recherche. L'algorithme pour construire ces ensembles reprend leur définition : on quadrille le disque de rayon 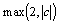 , appelé ensemble-cible, avec des points formant une grille de finesse fixée par l'argument pas, puis pour chaque point on effectue un certain nombre d'itérations (fixé par n), et on l'élimine dès qu'un de ses itérés sort de l'ensemble-cible. Les points restant forment alors une approximation par excès de
, appelé ensemble-cible, avec des points formant une grille de finesse fixée par l'argument pas, puis pour chaque point on effectue un certain nombre d'itérations (fixé par n), et on l'élimine dès qu'un de ses itérés sort de l'ensemble-cible. Les points restant forment alors une approximation par excès de  .
.
On peut déjà constater que les ensembles de prisonniers se subdivisent en deux catégories : ceux qui sont d'un seul tenant ("bloc" ou dendrite), c'est à dire connexes, et ceux qui sont effilochés en une myriade de morceaux déconnectés les uns des autres. Cette dichotomie se révélera très importante par la suite, mais il faut bien prendre garde au fait que les approximations informatiques faites dans ce chapitre ne permettent souvent pas de décider si tel ou tel ensemble de prisonniers est connexe ou pas.
B ] Les ensembles de Julia comme attracteurs d'IFS
L'idée est la suivante : comme tout point de l'ensemble des fugitifs, même très voisin de l'ensemble de Julia, a son orbite qui file à l'infini, on peut considérer que l'ensemble de Julia est un ensemble répulsif pour l'itérateur  , dès lors que le point initial est dans l'ensemble des fugitifs. En prenant un point de vue inverse, on peut le considérer comme attractif si, à partir d'un point de l'ensemble des fugitifs, on considère la suite des antécédents de ce point par
, dès lors que le point initial est dans l'ensemble des fugitifs. En prenant un point de vue inverse, on peut le considérer comme attractif si, à partir d'un point de l'ensemble des fugitifs, on considère la suite des antécédents de ce point par  . Seulement, comme
. Seulement, comme  est de degré 2, tout point admet en général deux antécédents, et on est donc amené à itérer l'IFS formé des deux transformations associant à tout
est de degré 2, tout point admet en général deux antécédents, et on est donc amené à itérer l'IFS formé des deux transformations associant à tout  les deux racines de l'équation
les deux racines de l'équation  .
.
J'ai donc modifié au minimum la procédure IFS vue dans FRACTALS.MWS (car les transformations de l'IFS ne sont plus affines) pour qu'elle puisse être réexploitée dans ce nouveau contexte ; en particulier, j'ai conservé le triangle comme compact de départ. La procédure julia2 est le résultat de cette transformation, et on pourra voir julia2(-1,9). Mais curieusement, on voit en fait tout l'ensemble des prisonniers se remplir de triangles de toutes formes, donnant finalement une silhouette de l'ensemble des prisonniers, alors qu'on n'aurait dû voir que l'ensemble de Julia !
Ceci tient au fait que dans IFS, je ne calculais en fait que les itérés des sommets des triangles, et que je remplissais le tout de couleur ensuite, utilisant le fait que l'image d'un triangle par une transformation affine reste un triangle. Ceci n'est évidemment plus vrai des applications utilisées dans julia2.
J'ai alors légèrement modifié julia2 en julia2bis, de manière à ce que les triangles ne soient plus remplis, ce qui donne un résultat satisfaisant, l'IFS s'appliquant maintenant à des triplets de points. Malheureusement, on est alors plus près du tracé de trois orbites simultanées que de celui des itérés d'un compact du plan.
La procédure julia3 corrige ce défaut en prenant au départ un cercle. Les commandes proposées permettent de s'assurer que cela fonctionne, du moins tant qu'aucun itéré ne passe par un point de discontinuité de la fonction sqrt du domaine complexe de MAPLE. Mais l'exécution est très lente, car chaque itération double l'ensemble de courbes à tracer, et le gros défaut de MAPLE est qu'il stocke les graphiques à tracer par un appel à plot ou display, attendant qu'ils soient tous calculés avant de commencer à les tracer, ce qui provoque une inflation des données en mémoire.
Enfin, julia4, qui est l'analogue d'IFS_ergodique, donne de bons résultats, sauf quant à présumer de la connexité des ensembles de Julia approximés. En effet, c'est là où les ensembles de Julia se font les plus fins que l'orbite ergodique à le moins de chance de passer...
On remarquera la forme particulière de  (un cercle) et
(un cercle) et  (un segment), qui sont les seuls ensembles de Julia à ne pas être des fractals. N'hésitez pas à cliquer sur le graphique et à faire apparaître les axes de coordonnées, ou à effectuer un zoom sur l'image par le menu view, zoom factor.
(un segment), qui sont les seuls ensembles de Julia à ne pas être des fractals. N'hésitez pas à cliquer sur le graphique et à faire apparaître les axes de coordonnées, ou à effectuer un zoom sur l'image par le menu view, zoom factor.
Il reste à commenter la structure fractale des ensembles de Julia. Leur apparente auto-similitude n'est bien entendu que statistique, puisque les transformations sur lesquelles s'appuie leur construction ne sont pas affines. Les ensembles de Julia ont cependant tous une propriété remarquable: si l'on fait un zoom sur une partie quelconque, aussi petite soit elle, - ce qui revient à choisir un disque ouvert du plan, en supposant l'intersection de ce disque avec l'ensemble de Julia non vide - alors un nombre fini d'itérations de  sur cette partie restitue l'ensemble de Julia tout entier !
sur cette partie restitue l'ensemble de Julia tout entier !
C ] L'ensemble de Mandelbrot
Une construction fine des ensembles de Julia pour divers paramètres montre clairement que certains sont connexes, tandis que les autres ne le sont pas. Dans certains cas, il est très difficile de le savoir, car les connexions entre les diverses parties de l'ensemble se font par un chemin très fin, voire un point unique.
En 1979, le mathématicien Benoît B. Mandelbrot décida d'étudier l'ensemble de points du plan qui porte son nom, qu'il définit comme l'ensemble  des paramètres pour lesquels l'ensemble de Julia correspondant est connexe. étant donné les moyens informatiques de l'époque, il était impensable de construire chaque ensemble de Julia pour décider quels paramètres étaient dans l'ensemble de Julia. Heureusement, il put mettre au point un algorithme plus simple.
des paramètres pour lesquels l'ensemble de Julia correspondant est connexe. étant donné les moyens informatiques de l'époque, il était impensable de construire chaque ensemble de Julia pour décider quels paramètres étaient dans l'ensemble de Julia. Heureusement, il put mettre au point un algorithme plus simple.
Commençons par la recherche des paramètres réels pour lesquels l'ensemble de Julia est connexe. Dans l'appendice du premier chapitre, nous avions montré l'équivalence de  avec
avec  , en posant
, en posant  et
et  . Cette dernière expression étant symétrique en
. Cette dernière expression étant symétrique en  par rapport à 1, on peut se limiter à
par rapport à 1, on peut se limiter à  . Si l'on cherche l'ensemble des prisonniers par
. Si l'on cherche l'ensemble des prisonniers par  pour ces valeurs de
pour ces valeurs de  , un calcul élémentaire montre déjà que toute orbite atteignant l'ensemble
, un calcul élémentaire montre déjà que toute orbite atteignant l'ensemble  diverge vers
diverge vers  . De plus, si
. De plus, si  , tout point de
, tout point de  voit son image, et par suite son orbite par
voit son image, et par suite son orbite par  demeurer dans
demeurer dans  . On peut donc en conclure que l'ensemble des réels prisonniers par
. On peut donc en conclure que l'ensemble des réels prisonniers par  pour
pour  est l'intervalle
est l'intervalle  .
.
Par contre, lorsque  , il existe un intervalle centré en
, il existe un intervalle centré en  dont les points ont leur image dans
dont les points ont leur image dans  . Tous les points de
. Tous les points de  dont l'orbite arrive à un moment dans cet intervalle sont donc dans l'ensemble des fugitifs. En calculant les antécédents des points de cet intervalle, puis les antécédents de ces antécédents, etc..., on va obtenir peu à peu (à la limite) l'ensemble des fugitifs de
dont l'orbite arrive à un moment dans cet intervalle sont donc dans l'ensemble des fugitifs. En calculant les antécédents des points de cet intervalle, puis les antécédents de ces antécédents, etc..., on va obtenir peu à peu (à la limite) l'ensemble des fugitifs de  , et par complémentarité dans
, et par complémentarité dans  celui des réels prisonniers. On s'aperçoit alors que l'ensemble des prisonniers est un ensemble non connexe, et qui plus est, du type ensemble de Cantor, c'est à dire formé carrément de points isolés !
celui des réels prisonniers. On s'aperçoit alors que l'ensemble des prisonniers est un ensemble non connexe, et qui plus est, du type ensemble de Cantor, c'est à dire formé carrément de points isolés !
La commande julia_réel(n,a) permet de construire l'approximation de l'ensemble des prisonniers obtenue après le nombre n de calculs d'antécédents pour le paramètre a. On peut voir ainsi que  correspond à un ensemble des prisonniers connexe, tandis que
correspond à un ensemble des prisonniers connexe, tandis que  correspond à un ensemble de prisonniers formé d'un ensemble type Cantor.
correspond à un ensemble de prisonniers formé d'un ensemble type Cantor.
La construction sur le même graphique de la parabole d'itération permet de comprendre pourquoi ce changement se produit au passage de  : en effet, dès que la parabole a son sommet au-dessus de la droite
: en effet, dès que la parabole a son sommet au-dessus de la droite  , une porte est ouverte permettant aux fugitifs de s'échapper.
, une porte est ouverte permettant aux fugitifs de s'échapper.
On peut conclure que pour  , l'ensemble des prisonniers est connexe si et seulement si le point
, l'ensemble des prisonniers est connexe si et seulement si le point  n'est pas fugitif.
n'est pas fugitif.
Passons maintenant à  , pour
, pour  réel. On déduit immédiatement de la formule
réel. On déduit immédiatement de la formule  que l'ensemble des réels prisonniers est connexe si et seulement si
que l'ensemble des réels prisonniers est connexe si et seulement si  . Mais on déduit également de la correspondance
. Mais on déduit également de la correspondance  que l'ensemble des réels prisonniers est connexe si et seulement si le point
que l'ensemble des réels prisonniers est connexe si et seulement si le point  n'est pas fugitif.
n'est pas fugitif.
Ceci est équivalent à dire que le nombre  lui-même n'est pas fugitif, puisqu'il est l'image de zéro.
lui-même n'est pas fugitif, puisqu'il est l'image de zéro.
On est donc amené à conjecturer, en passant audacieusement à  , que :
, que :
 l'orbite de
l'orbite de  est bornée.
est bornée.
Pour justifier (sans la démontrer !) cette conjecture, rappelons que l'origine est centre de symétrie de tout ensemble de Julia. Or, lorsque nous avons construit l'ensemble des prisonniers par encerclement progressif (voir julia1), nous sommes partis de l'ensemble-cible formé du disque de rayon 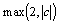 , donc d'un ensemble connexe, et à chaque étape (passage de julia1(c,n,pas) à julia1(c,n+1,pas)) pouvaient se produire deux alternatives : ou le nouvel ensemble restait connexe, ou il se subdivisait en deux, l'origine étant alors en-dehors. Dans le deuxième cas, l'étape suivante fait apparaître quatre morceaux, puis huit, etc... Par analogie au cas réel discuté plus haut, on dit que l'ensemble des prisonniers est une poussière de Cantor.
, donc d'un ensemble connexe, et à chaque étape (passage de julia1(c,n,pas) à julia1(c,n+1,pas)) pouvaient se produire deux alternatives : ou le nouvel ensemble restait connexe, ou il se subdivisait en deux, l'origine étant alors en-dehors. Dans le deuxième cas, l'étape suivante fait apparaître quatre morceaux, puis huit, etc... Par analogie au cas réel discuté plus haut, on dit que l'ensemble des prisonniers est une poussière de Cantor.
C'est l'idée encadrée ci-dessus que Mandelbrot a utilisée en 1979 pour obtenir une première image de  , et que nous reprenons dans mandelbrot1 : on quadrille le plan avec une finesse définie par pas, et pour chaque noeud
, et que nous reprenons dans mandelbrot1 : on quadrille le plan avec une finesse définie par pas, et pour chaque noeud  de la grille obtenue, on le conserve si et seulement si l'orbite de
de la grille obtenue, on le conserve si et seulement si l'orbite de  par
par  ne diverge pas vers l'infini.
ne diverge pas vers l'infini.
On sait déjà que si  , alors
, alors  , ce qui entraîne comme on l'a vu l'appartenance de
, ce qui entraîne comme on l'a vu l'appartenance de  à l'ensemble des fugitifs pour
à l'ensemble des fugitifs pour  , et donc sa non-appartenance à l'ensemble de Mandelbrot. On peut donc se contenter de tester les orbites des points du disque de rayon 2. Pour ce faire, on calcule les itérés de
, et donc sa non-appartenance à l'ensemble de Mandelbrot. On peut donc se contenter de tester les orbites des points du disque de rayon 2. Pour ce faire, on calcule les itérés de  , et on élimine
, et on élimine  dès qu'un itéré sort de l'ensemble-cible formé du disque de rayon
dès qu'un itéré sort de l'ensemble-cible formé du disque de rayon  . On ne peut dans la pratique calculer qu'un nombre fini d'itérés, donné par le nombre
. On ne peut dans la pratique calculer qu'un nombre fini d'itérés, donné par le nombre  , ce qui donne une approximation par excès de l'ensemble de Mandelbrot.
, ce qui donne une approximation par excès de l'ensemble de Mandelbrot.
Une méthode plus efficace, implantée dans mandelbrot2, permet de construire une approximation de la frontière de l'ensemble de Mandelbrot. On part d'un triangle dont deux côtés intersectent la frontière, et on fabrique une chaîne de triangles ayant la même propriété en effectuant, pour trouver le triangle suivant, une symétrie centrale de centre le milieu de l'un des côtés sur le triangle courant. Cette chaîne revient nécessairement au triangle de départ, après avoir tourné le long de la frontière de  . La procédure mandelbrot2 exploite la symétrie de l'ensemble de Mandelbrot par rapport à l'axe des réels, en commençant le processus sur cet axe, et en l'arrêtant dès que la partie supérieure de
. La procédure mandelbrot2 exploite la symétrie de l'ensemble de Mandelbrot par rapport à l'axe des réels, en commençant le processus sur cet axe, et en l'arrêtant dès que la partie supérieure de  a été calculée ; il ne reste plus alors qu'à compléter par symétrie. Cette méthode ne fonctionne plus très bien lorsque la précision demandée devient trop grande, car l'orbite des paramètres proches de l'ensemble de Mandelbrot met beaucoup de temps à sortir de l'ensemble-cible.
a été calculée ; il ne reste plus alors qu'à compléter par symétrie. Cette méthode ne fonctionne plus très bien lorsque la précision demandée devient trop grande, car l'orbite des paramètres proches de l'ensemble de Mandelbrot met beaucoup de temps à sortir de l'ensemble-cible.
D ] Les propriétés fascinantes de l'ensemble de Mandelbrot

Commençons maintenant notre voyage dans l'ensemble de Mandelbrot, ou plutôt autour de cet ensemble, puisque comme le montre la représentation ci-contre de cet ensemble, c'est surtout la frontière de  qui présente un intérêt. Cette frontière est d'ailleurs une courbe fractale de dimension 2, ce qui prouve son extraordinaire complexité !
qui présente un intérêt. Cette frontière est d'ailleurs une courbe fractale de dimension 2, ce qui prouve son extraordinaire complexité !
De façon sommaire,  est composée de droite à gauche d'un morceau en forme de coeur, puis d'un disque, puis de morceaux de plus en plus petits, tous ces morceaux étant tangents entre eux en des paramètres réels, et devenant très vite invisibles.
est composée de droite à gauche d'un morceau en forme de coeur, puis d'un disque, puis de morceaux de plus en plus petits, tous ces morceaux étant tangents entre eux en des paramètres réels, et devenant très vite invisibles.
Cette succession de morceaux semble ensuite faire place à une ligne droite, sur laquelle on discerne cependant des protubérances éparses.
Sur les frontières de ces morceaux poussent régulièrement des bourgeons plus ou moins gros, qui semblent eux-mêmes dotés d'une structure très complexe, et qui s'achèvent en filaments.
Nous allons d'abord rappeler une propriété d'analyse complexe : lorsque  est un point fixe d'une application
est un point fixe d'une application  dérivable de
dérivable de  dans
dans  , alors ce point fixe est attractif si
, alors ce point fixe est attractif si  , répulsif si
, répulsif si  , et on dit qu'il est indifférent si
, et on dit qu'il est indifférent si  .
.
Dans le cas de  , il y a deux points fixes (éventuellement confondus), et leur nature est déterminée par le double de leur module. De plus, les points fixes de
, il y a deux points fixes (éventuellement confondus), et leur nature est déterminée par le double de leur module. De plus, les points fixes de  sont
sont  ,
,  désignant l'une des racines carrées de
désignant l'une des racines carrées de  . Il s'ensuit que
. Il s'ensuit que  , ce qui entraîne que, hormis le cas particulier
, ce qui entraîne que, hormis le cas particulier  où les deux points fixes sont confondus en un seul point indifférent, si l'un des points fixes est attractif ou indifférent, l'autre est répulsif (attention, les deux peuvent être répulsifs).
où les deux points fixes sont confondus en un seul point indifférent, si l'un des points fixes est attractif ou indifférent, l'autre est répulsif (attention, les deux peuvent être répulsifs).
Ce résultat très simple, et la possibilité que nous avons de pouvoir comparer à  pour
pour  , vont nous permettre de comprendre la signification des observations ci-dessus.
, vont nous permettre de comprendre la signification des observations ci-dessus.
Intéressons-nous d'abord au morceau le plus gros, celui en forme de coeur (les bourgeons exclus). Son intersection avec la droite réelle est  , ce qui correspond à
, ce qui correspond à  pour
pour  . Ces valeurs correspondent précisément sur le diagramme de Feigenbaum à l'existence d'un unique point fixe attractif. Nous pouvons donc conjecturer que ce morceau contient les paramètres
. Ces valeurs correspondent précisément sur le diagramme de Feigenbaum à l'existence d'un unique point fixe attractif. Nous pouvons donc conjecturer que ce morceau contient les paramètres  pour lesquels existe un point attractif.
pour lesquels existe un point attractif.
C'est facile à vérifier : paramétrons l'ensemble des paramètres  définis par
définis par  . En posant
. En posant  , on obtient l'ensemble
, on obtient l'ensemble 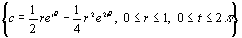 . La frontière de cet ensemble, qui est aussi l'ensemble des paramètres pour lesquels il existe un point fixe indifférent, est la courbe d'équations paramétriques
. La frontière de cet ensemble, qui est aussi l'ensemble des paramètres pour lesquels il existe un point fixe indifférent, est la courbe d'équations paramétriques  . En ramenant l'origine au point
. En ramenant l'origine au point  , et en passant en coordonnées polaires, on reconnaît l'équation d'une cardioïde
, et en passant en coordonnées polaires, on reconnaît l'équation d'une cardioïde  .
.
Remarque anecdotique : si l'on choisit un ensemble-cible, et que pour le paramètre  (qui est extérieur à l'ensemble de Mandelbrot si
(qui est extérieur à l'ensemble de Mandelbrot si  ), on calcule le nombre d'itérations
), on calcule le nombre d'itérations  nécessaires à partir de la valeur initiale
nécessaires à partir de la valeur initiale  pour que l'orbite sorte de l'ensemble-cible, on constate que
pour que l'orbite sorte de l'ensemble-cible, on constate que  au voisinage de zéro...
au voisinage de zéro...
Continuons avec l'étude de ce qui semble être un disque tangent à la cardioïde précédente au point  . Ce disque semble centré en
. Ce disque semble centré en  . Les paramètres réels correspondant sont ceux compris entre
. Les paramètres réels correspondant sont ceux compris entre  , ce qui nous ramène à
, ce qui nous ramène à  pour
pour  . Or
. Or  Ceci correspond exactement au point où se produit la deuxième bifurcation de Feigenbaum ! L'intervalle
Ceci correspond exactement au point où se produit la deuxième bifurcation de Feigenbaum ! L'intervalle  correspondant à la phase où l'itérateur quadratique possédait un cycle attractif de période 2, on est amené à penser que notre disque correspond à tous les paramètres pour lesquels
correspondant à la phase où l'itérateur quadratique possédait un cycle attractif de période 2, on est amené à penser que notre disque correspond à tous les paramètres pour lesquels  possède un cycle attractif de période 2. Un calcul analogue au précédent, utilisant le fait que
possède un cycle attractif de période 2. Un calcul analogue au précédent, utilisant le fait que  possède alors deux points attractifs distincts, permet de vérifier effectivement que l'ensemble des paramètres de ce type est bien le disque de centre
possède alors deux points attractifs distincts, permet de vérifier effectivement que l'ensemble des paramètres de ce type est bien le disque de centre  et de rayon
et de rayon  .
.
On imagine facilement la suite : chaque nouvelle forme géométrique tangente à gauche à la précédente va correspondre à un doublement de la période du cycle attractif, exactement selon le même schéma que dans le phénomène des bifurcations de Feigenbaum, et ce jusqu'au paramètre  , où
, où  désigne le point de Feigenbaum. De plus, les petites protubérances que l'on voit entre ce point
désigne le point de Feigenbaum. De plus, les petites protubérances que l'on voit entre ce point  et le point le plus à gauche
et le point le plus à gauche  correspondent exactement aux fenêtres périodiques que l'on observait dans le reflet chaotique de l'arbre des périodes doublantes du diagramme de Feigenbaum.
correspondent exactement aux fenêtres périodiques que l'on observait dans le reflet chaotique de l'arbre des périodes doublantes du diagramme de Feigenbaum.
On peut observer de surcroît que dans une partie de  correspondant à un cycle attractif de période
correspondant à un cycle attractif de période , les ensembles de prisonniers des paramètres de cette partie sont faits d'au moins
, les ensembles de prisonniers des paramètres de cette partie sont faits d'au moins  parties, raccordées l'une à l'autre en un seul point, et les points du cycle attractif se répartissent dans ces parties. Pour un paramètre de la frontière d'une de ces parties, un point du cycle attractif se trouve alors en l'un des points de connexion. Ceci éclaire mieux la dynamique à l'intérieur des ensembles de prisonniers connexes.
parties, raccordées l'une à l'autre en un seul point, et les points du cycle attractif se répartissent dans ces parties. Pour un paramètre de la frontière d'une de ces parties, un point du cycle attractif se trouve alors en l'un des points de connexion. Ceci éclaire mieux la dynamique à l'intérieur des ensembles de prisonniers connexes.
Nous avons ainsi éclairé la structure globale de l'ensemble de Mandelbrot, mais absolument pas celle des bourgeons qui poussent un peu partout sur sa frontière, connectés aux parties principales uniquement en un point. Nous savons déjà que les points de la frontière des différentes parties de  sont des paramètres
sont des paramètres  correspondant à l'existence d'un attracteur périodique indifférent. Pour essayer de comprendre ce qui se passe, nous allons étudier les paramètres situés sur la cardioïde, qui correspondent donc à l'existence d'un point attractif indifférent. On a donc, en ce point
correspondant à l'existence d'un attracteur périodique indifférent. Pour essayer de comprendre ce qui se passe, nous allons étudier les paramètres situés sur la cardioïde, qui correspondent donc à l'existence d'un point attractif indifférent. On a donc, en ce point 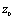 ,
,  . On dit alors que
. On dit alors que 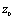 est rationnellement (respect. irrationnellement) indifférent si
est rationnellement (respect. irrationnellement) indifférent si  est commensurable (respect. incommensurable) avec
est commensurable (respect. incommensurable) avec .
.
Dans les deux cas, la dynamique au voisinage du point fixe peut être grossièrement décrite comme une rotation autour du point fixe.
On démontre que tous les points de la cardioïde correspondant à un point fixe rationnellement indifférent sont des points de connexion de bourgeons (ce qui prouve la densité des bourgeons sur la cardioïde), et les ensembles de Julia correspondant contiennent ce point fixe. Par exemple, les points correspondant aux paramètres  de la cardioïde
de la cardioïde  sont des points de départ de bourgeons dont le "noyau" contient des paramètres correspondant à l'existence d'un cycle attractif de période
sont des points de départ de bourgeons dont le "noyau" contient des paramètres correspondant à l'existence d'un cycle attractif de période  . Plus surprenant encore : le bourgeon principal entre deux bourgeons de période respective
. Plus surprenant encore : le bourgeon principal entre deux bourgeons de période respective  est de période
est de période  . Des règles analogues sont vraies pour les autres parties principales de
. Des règles analogues sont vraies pour les autres parties principales de  , ainsi que pour les bourgeons sur les bourgeons, etc...
, ainsi que pour les bourgeons sur les bourgeons, etc...
Par contre, ce qui se passe pour les points irrationnellement indifférents correspondant à  est plus compliqué : si
est plus compliqué : si  vérifie la propriété d'être mal approché par les rationnels, c'est à dire qu'il vérifie
vérifie la propriété d'être mal approché par les rationnels, c'est à dire qu'il vérifie  , alors on dit que l'ensemble de Julia correspondant est un disque de Siegel. La dynamique autour du point fixe indifférent y est caractérisée par des courbes globalement invariantes sur lesquelles l'itération agit comme une rotation. On pourra le tester avec le nombre d'or
, alors on dit que l'ensemble de Julia correspondant est un disque de Siegel. La dynamique autour du point fixe indifférent y est caractérisée par des courbes globalement invariantes sur lesquelles l'itération agit comme une rotation. On pourra le tester avec le nombre d'or  . Quant à la forme des ensembles de Julia correspondant à l'autre type de points irrationnellement indifférents, elle est mal connue, et ces ensembles de Julia sont difficiles à visualiser car, bien que connexes, ils ne sont pas localement connexes ; ceci signifie qu'il existe des points de ces ensembles dont il existe un voisinage ne contenant aucune intersection connexe avec l'ensemble de Julia !
. Quant à la forme des ensembles de Julia correspondant à l'autre type de points irrationnellement indifférents, elle est mal connue, et ces ensembles de Julia sont difficiles à visualiser car, bien que connexes, ils ne sont pas localement connexes ; ceci signifie qu'il existe des points de ces ensembles dont il existe un voisinage ne contenant aucune intersection connexe avec l'ensemble de Julia !
Les phénomènes qui se produisent aux points des frontières d'autres parties de l'ensemble de Mandelbrot sont comparables, mis à part qu'au lieu de points fixes indifférents, on a des cycles périodiques indifférents.
Tentons maintenant de cerner la nature des espèces de filaments qui semblent pousser à la fin de chaque bourgeonnement. Lorsqu'on agrandit ces zones de l'ensemble de Mandelbrot, on découvre des ensembles qui ressemblent étrangement à des ensembles de prisonniers connexes de tout type : dendrites ou d'intérieur non vide. En fait, le théorème de Tan Lei ( 1989 ) affirme qu'en certains points particuliers  de l'ensemble de Mandelbrot, il existe une similitude
de l'ensemble de Mandelbrot, il existe une similitude  de centre
de centre  , et un disque
, et un disque  de centre
de centre  , tels que l'application successive de
, tels que l'application successive de  respectivement à
respectivement à  et
et  entraîne la convergence de la figure itérée vers un ensemble limite égal respectivement à
entraîne la convergence de la figure itérée vers un ensemble limite égal respectivement à  et
et  , avec
, avec  et
et  semblables.
semblables.
Un point vérifiant cette propriété est appelé un point de Misiurewicz. Il s'agit tout simplement d'un point  dont l'orbite par
dont l'orbite par  est périodique à partir d'un certain rang, mais dont la période ne contient pas l'origine. Les points de Misiurewicz étant dense à la frontière de l'ensemble de Mandelbrot, cela explique que partout le long de cette frontière l'on trouve des images ressemblant beaucoup à des ensembles de prisonniers. Les filaments que l'on distingue ressemblent pour leur part à des dendrites.
est périodique à partir d'un certain rang, mais dont la période ne contient pas l'origine. Les points de Misiurewicz étant dense à la frontière de l'ensemble de Mandelbrot, cela explique que partout le long de cette frontière l'on trouve des images ressemblant beaucoup à des ensembles de prisonniers. Les filaments que l'on distingue ressemblent pour leur part à des dendrites.
Pour résumer, on dit souvent que la frontière de  est un catalogue des ensembles de Julia.
est un catalogue des ensembles de Julia.
Mais ce n'est pas tout : si l'on agrandit n'importe quelle portion de la frontière de l'ensemble de Mandelbrot, on observe à n'importe quelle échelle des ensembles qui ressemblent eux aussi à l'ensemble de Mandelbrot. Ceci semble en contradiction avec la densité des points de Misiurewicz et le théorème de Tan Lei. En fait, cela provient du fait que chaque fois qu'on applique la similitude  au voisinage d'un point de Misiurewicz, les petits ensembles de Mandelbrot qui se trouvent cachés dans l'image obtenue sont indiscernables, et sont vus comme des points. Ceci montre en passant que la taille des petits ensembles de Mandelbrot qui se trouvent au voisinage d'un point de Misiurewicz n'est pas arbitraire : sinon, on finirait par en apercevoir en effectuant les itérations successives de
au voisinage d'un point de Misiurewicz, les petits ensembles de Mandelbrot qui se trouvent cachés dans l'image obtenue sont indiscernables, et sont vus comme des points. Ceci montre en passant que la taille des petits ensembles de Mandelbrot qui se trouvent au voisinage d'un point de Misiurewicz n'est pas arbitraire : sinon, on finirait par en apercevoir en effectuant les itérations successives de  .
.